
题目列表(包括答案和解析)
1、设集合A是一个非空的实数集,对于A内 ,按照确定的对应法则f,都有 与它对应,则这种对应关系叫做集合A上的一个函数,记作 .
2.会用集合与对应语言来刻画函数,了解构成函数的要素.
[知识再现]在初中,已学习了变是与函数的概念,在一个变化过程中有两个变量x和y,如果给定一个x值,相应地就确定唯一的一个y值,那么我们就称y是x的函数,其中x是自变量,y是因变量.
[概念探究]
自学课本P29-P31,填充以下空格.
1.理解函数的概念;
2.1.1 函数 学案(1)
[预习要点及要求]
4、设集合A={2, 4, 6, 8, 10}, B={1, 9, 25, 49, 81, 100},下面的对应关系f能构成A到B的映射的是( )
A、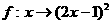 B、
B、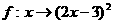
C、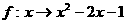 D、
D、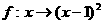
3、为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b, 2b+c, 2c+3d, 4d,例如,明文1, 2, 3,4对应密文5, 7, 18, 16.当接收方收到密文14, 9, 23, 28时,则解密得到的明文为( )
A、4, 6, 1, 7 B、7, 6, 1, 4 C、6, 4, 1, 7 D、1, 6, 4, 7
2、区间[0,m]在映射f:x→2x+m所得的象集区间为[a, b],若区间[a, b]的长度比区间[0, m]的长度大5,则m等于( )
A、5 B、10 C、2.5 D、1
1、在给定的映射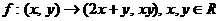 的条件下,点
的条件下,点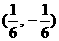 的原象是( )
的原象是( )
A、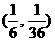 B、
B、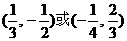 C、
C、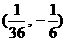 D、
D、
4、由映射的定义可以看出,映射是 概念的推广, 是一种特殊的映射,要注意构成函数的两个集合A、B必须是 .
完成课本P34-35,例4、例5、例6、例7.
[总结点拨]
从集合A到集合B的映射,允许多个元素对应一个元素,而不允许一个元素对应多个元素.
[例题讲解]
例1、判断下列对应哪些是由A到B的映射?为什么?
(1)A=R,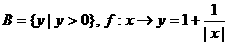 ;
;
(2)A=R,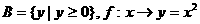 ;
;
(3)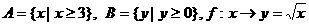 (4)A=Z,B=Q,
(4)A=Z,B=Q,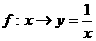
例2、已知集合A=R,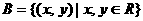 ,
,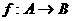 是从A到B的映射,
是从A到B的映射,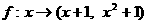 ,求A中元素
,求A中元素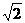 的象和B中元素
的象和B中元素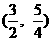 的原象.
的原象.
例3、已知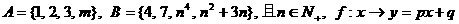 是从A到B的一个一一映射,已知1的象是4,7的原象是2,求p, q, m, n的值.
是从A到B的一个一一映射,已知1的象是4,7的原象是2,求p, q, m, n的值.
[当堂达标]
3、如果映射f是集合A到B的映射,并且对于B中的任何一个元素,在集合A中都有且只有一个原象,这时我们说这两个集合之间存在 ,并称这个映射为集合A到集合B的 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com