
题目列表(包括答案和解析)
3.★(2005重庆)圆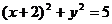 关于原点(0,0)对称的圆的方程为( )。
关于原点(0,0)对称的圆的方程为( )。
A.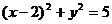 B.
B.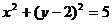
C.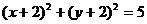 D.
D.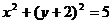
2.解析:直线过圆心时才将圆平分,将圆心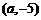 代入直线方程
代入直线方程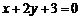 ,解得
,解得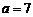 .
.
答案:B
2.★直线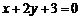 将圆
将圆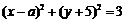 平分,则
平分,则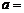 ( )。
( )。
A.13 B.7 C.-13 D.以上答案都不对
1.解析:因为圆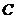 经过坐标原点,所以圆
经过坐标原点,所以圆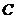 的半径
的半径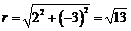 .因此,所求圆的方程是
.因此,所求圆的方程是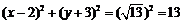 .
.
答案:B
1.★圆心是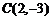 ,且经过原点的圆的方程为( ).
,且经过原点的圆的方程为( ).
A.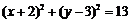 B.
B.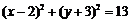
C.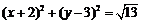 D.
D.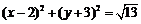
1.1.4投影与直观图(1课时)
执笔人: 韩邦平 审核人:李峰
|
课题 学时 |
1.1.4投影与直观图 (1课时) |
|
学习 目标 |
1.通过实物模型观察大量立体图形(如一些标志性建筑)的平行投影,了解空间图形的平行投影的概念及其性质; 2.会用斜二侧画法画出空间图形的直观图; 3.了解中心投影的概念. |
|
学法 指导 |
1. 注意与身边的实物相结合,提高空间想象能力; 2. 关键概念:平行投影、直观图、中心投影; 3. 关键原理:平行投影的性质、斜二测画法。 |
|
诊 断 训 练 |
(1)
下列命题中正确的是( ) A.矩形的平行投影一定是矩形 B.梯形的平行投影一定是梯形 C.两条相交直线的投影可能平行D.一条线段中点的平行投影仍是这条线段投影的中点  (2)两条不平行的直线,其平行投影不可能是( ) (2)两条不平行的直线,其平行投影不可能是( )A.两条平行直线B.一点和一条直线 C.两条相交直线D.两个点 (3)水平放置的△ABC的斜二测直观图如图所示,已知 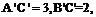 则AB边上的中线的实际长度为_________. 则AB边上的中线的实际长度为_________. |
|
知 识 链 接 |
(1)平行投影的概念 已知图形F,直线l与平面 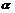 相交,过F上任意一点M作直线 相交,过F上任意一点M作直线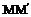 平行于l,交平面 平行于l,交平面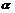 于点 于点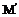 ,则 ,则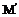 叫做_________________________,如果图形F上的所有点在平面 叫做_________________________,如果图形F上的所有点在平面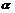 内关于直线l的平行投影构成图形 内关于直线l的平行投影构成图形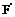 ,则 ,则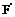 叫做___________________.平面 叫做___________________.平面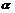 叫做______,l叫做_____ 叫做______,l叫做_____(2) 平行投影的性质 当图形中的直线或线段不平行于投射线时,平行投影具有下列性质: ①______________________________; ②______________________________; ③______________________________; ④______________________________; ⑤___________________________________________________________。 (3)用来表示空间图形的___________,叫做空间图形的直观图。 (4)斜二测画法的主要特征 ①______________________________;②______________________________; ③______________________________。 (5)投影分为__________和___________. |
|
问题探究 |
例1画出水平放置的正六边形的直观图。 例2画出正六棱锥P-ABCDEF的直观图(尺寸自定)。 例3 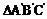 是水平放置的平面图形的斜二测直观图,将其恢复成原图形。 是水平放置的平面图形的斜二测直观图,将其恢复成原图形。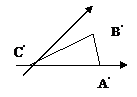 |
|
分层训练 |
A级(基础) 1. 一个图形的平行投影是一条线段,这个图形不可能是( ) A.线段B.直线C.圆D.梯形 2.利用斜二测画法画水平放置的直观图时有( ) A.正三角形的直观图是正三角形B.平行四边形的直观图是平行四边形 C.相等的线段在直观图中仍相等D.全等三角形的直观图一定全等 3.已知一个正方形的斜二测直观图是一个平行四边形,该平行四边形有一边长为4,则此正方形的面积是( ) A.16 B.64 C.16或64 D.都不对 4.一个正方形的平行投影可能是__________ |
|
B级(中等) 1.画出一个锐角为 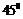 的平行四边形的直观图。 的平行四边形的直观图。2.如图所示的直观图的原平面图形是( ) 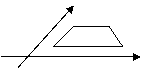  A.任意三角形B.直角梯形C.任意四边形D.平行四边形 |
|
|
C级(拓展) 1.已知正三角形ABC的边长为a,求 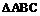 的平面直观图的面积。 的平面直观图的面积。2.已知 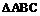 的平面直观图是边长为a的正三角形,那么原三角形的面积是____. 的平面直观图是边长为a的正三角形,那么原三角形的面积是____. |
|
|
课后反馈 |
1.一个水平放置的平面图形的斜二测直观图是一个底角为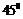 ,腰和上底均为1的等腰梯形,画出原平面图形并求原平面图形的面积。 ,腰和上底均为1的等腰梯形,画出原平面图形并求原平面图形的面积。2.正方形 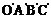 的边长为1cm,它是水平放置的一个平面图形 的边长为1cm,它是水平放置的一个平面图形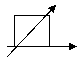  的直观图,画出原图形,并求原图形的周长。 的直观图,画出原图形,并求原图形的周长。 |
9、函数f(x) = 2x - 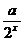 .
.
(1)将y = f(x)的图象向右平移2个单位,得到函数y = g(x)的图象,求函数y = g(x)的解析式;
(2)函数y = h(x)与y = g(x)的图象关于直线y = 1对称,求函数y = h(x)的解析式;
(3)设F(x) = 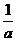 f(x) + h(x),已知F(x)的最小值是m,且m> 2+
f(x) + h(x),已知F(x)的最小值是m,且m> 2+ 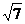 ,求实数a的取值范围。
,求实数a的取值范围。
8、已知函数f(x) = log2(x2 + 1)(x≥0),g(x) = 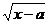 (a∈R)。
(a∈R)。
(1)试求函数f(x)的反函数f-1(x);
(2)函数h(x) = f-1(x)+ g(x),求h(x)的定义域,并判断函数h(x)的增减性;
(3)若(2)中函数h(x),有h(x)≥2在定义域内恒成立,求a的范围。
7、(1)已知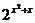 ≤
≤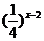 ,求函数y = 2x –2-x的值域;
,求函数y = 2x –2-x的值域;
(2)已知函数f(x) = log3x +2(x∈[1,9]),求函数y = [f(x)]2 + f(x2)的最大值。
6、设a>0且a≠1,若loga2< log2a,则a的取值范围是___________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com