
题目列表(包括答案和解析)
2.不等式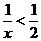 的解集是
.
的解集是
.
例1 解不等式: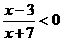 .
.
变式1:解不等式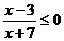
变式3:解不等式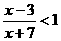
归纳分式不等式的解法:
(1) 化分式不等式为标准型:
(2) 将分式不等式转化为整式不等式求解如:
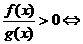
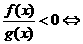
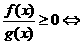
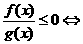
练习:
1.不等式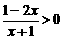 的解集是
。
的解集是
。
(1)设不等式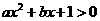 的解集为
的解集为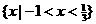 ,求
,求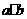
(2)已知二次不等式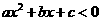 的解集为
的解集为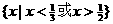 ,求关于
,求关于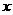 的不等式
的不等式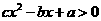 的解集.
的解集.
5.2 简单的分式不等式和高次不等式的解法
解不等式
(1)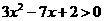 (2)
(2)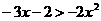 . (3)
. (3)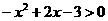 .
.
(4)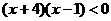 (5)
(5)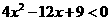 (6)
(6)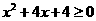
(7)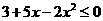 (8)
(8)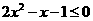 (9)
(9) 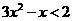
|
|
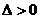 |
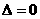 |
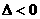 |
二次函数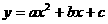 ( 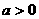 )的图象 )的图象 |
|
|
|
一元二次方程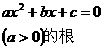 |
|
|
|
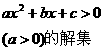 |
|
|
|
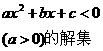 |
|
|
|
思考:(1)a<0时如何解不等式?
(2)解一元二次不等式的步骤:
① 将二次项系数化为“+”:y=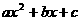 >0(或<0)(a>0)
>0(或<0)(a>0)
② 计算判别式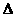 ,分析不等式的解的情况:
,分析不等式的解的情况:
③ 写出解集
(1)画出函数
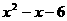 的图象;当x取什么值时,函数值大于0; 、x取什么值时,函数值小于0
的图象;当x取什么值时,函数值大于0; 、x取什么值时,函数值小于0
(2)画出函数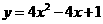 的图象;当x取何值时,函数值大于0;
的图象;当x取何值时,函数值大于0;
x取什么值时,函数值大于等于0;x取什么值时,函数值小于0
(3)画出函数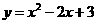 的图象;
的图象;
当x取什么值时,函数值大于0; x取什么值时,函数值小于0
5.1一元二次不等式的解法
5.已知二次函数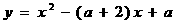
(1)求证:不论a为任何实数,函数的图象与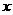 轴都有两个交点;
轴都有两个交点;
(2)试求:当a为何值时,函数图象与x轴的两个交点之间的距离等于2;
(3)函数图象与x轴的两个交点分别位于x=2的两侧,m的取值如何?
第五节 不等式的解法
4.函数y=2x2+4x-5中,当-3≤x<2时,则y值的取值范围是 ( )
(A)-3≤y≤1 (B)-7≤y≤1
(C)-7≤y≤11 (D)-7≤y<11
3.函数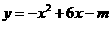 的值恒小于0,那么实数m的值满足( )
的值恒小于0,那么实数m的值满足( )
A.m>9 B.m= 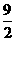 C.m<9 D.m>
C.m<9 D.m>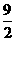
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com