
题目列表(包括答案和解析)
4..设点(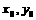 )在圆
)在圆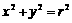 的外部,则直线
的外部,则直线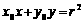 与圆的位置关系是( )
与圆的位置关系是( )
A.相交 B.相切 C. 相离 D.不确定
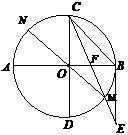
在⊙O中,直径AB、CD互相垂直,BE切⊙O于B,且BE=BC,CE交AB于F,交⊙O于M,连结MO并延长,交⊙O于N,则下列结论中,正确的是( )
A. CF=FM B. OF=FB C. 的度数是22.5° D. BC∥MN
3.给出下列四个命题,其中是真命题的为( )
①角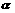 一定是直线
一定是直线 的倾斜角;
的倾斜角;
②点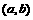 关于直线
关于直线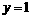 的对称点的坐标是
的对称点的坐标是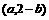 ;
;
③与坐标轴距离相等的点的轨迹方程是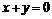 ;
;
④直线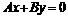 与圆
与圆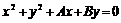 相切.
相切.
A.(1)、(2) B.(3)、(4) C.(1)、(3) D.(2)、(4)
2..倾斜角为60o,且过原点的直线被圆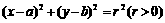 截得的弦长恰等于圆的半径,则
截得的弦长恰等于圆的半径,则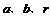 满足的条件是( )
满足的条件是( )
A.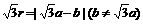 B.
B. 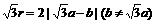
C. 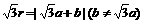 D.
D. 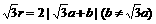
1.曲线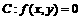 关于直线
关于直线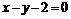 对称的曲线C′的方程为(
)
对称的曲线C′的方程为(
)
A.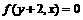 B.
B.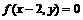 C.
C.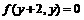 D.
D.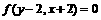
设圆圆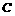 :
: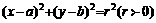 ; 直线
; 直线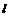 :
: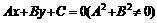 ;
;
圆心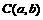 到直线
到直线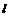 的距离
的距离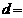 .
.
①
,与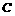 相切
相切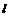 ;
;
若两圆相切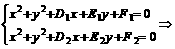 ,则相减为
,则相减为
②
,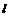 与
与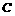 相交;
相交;
③
,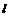 与
与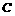 相离.
相离.
由代数特征判断:方程组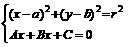 用代入法,得关于
用代入法,得关于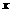 (或
(或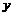 )的一元二次方程,其判别式为
)的一元二次方程,其判别式为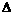 ,则:
,则:
与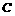 相切;
相切;
与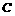 相交;
相交;
与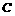 相离.
相离.
2.解:设圆C的方程为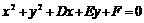 ,
,
由于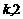 为方程
为方程 的两根
的两根
∴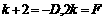 即
即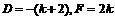
又因为圆过点R(0,1),故1+E+F=0, ∴E=-2k-1
∴圆的方程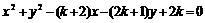
圆心C坐标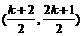 ∵圆在点P的切线斜率为1 ∴
∵圆在点P的切线斜率为1 ∴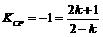 解得
解得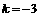
∴所求圆的方程为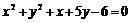
直线与圆的位置关系
1.解:设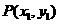 、
、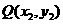 ,
,
由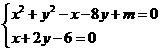 ,消去
,消去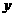 得:
得: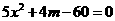 , ①
, ①
由题意:方程①有两个不等的实数根,∴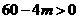 ,
,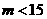 ,
,
由韦答定理: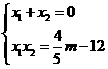 ,
,
∵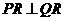 ,∴
,∴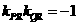 ,∴
,∴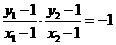 ,即
,即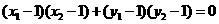 ,
,
即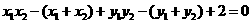 ,
②
,
②
∵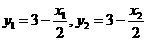 ,∴
,∴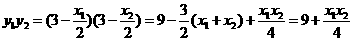 ,
,
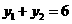 ,代入②得:
,代入②得: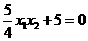 ,即
,即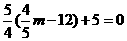 ,
,
∴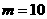 ,适合
,适合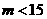 ,所以,实数
,所以,实数 的值为
的值为 .
.
1. -2或4 ; 2. 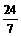 ;
3.
;
3. 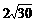
解答题:
2.圆C通过不同的三点P(K,O)、Q(2, 0)、R(0,1),已知圆C在点P的切线斜率为1,试求圆C的方程.
答案详解:
基础知识: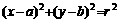 ;
;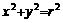 ;
;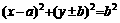 ;
;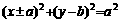 ;
;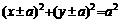 ;
;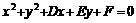 ;
;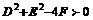 ;
;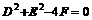 ;
;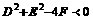 ;
;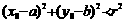 ;
;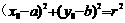 ;
;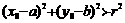
选择题:C;C;B;D;A;A
填空题:
1.已知圆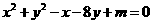 与直线
与直线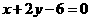 相交于
相交于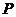 、
、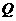 两点,定点
两点,定点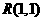 若
若
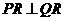 ,求实数
,求实数 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com