
题目列表(包括答案和解析)
4.集合的表示方法
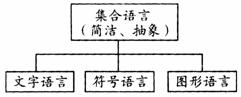
集合的表示方法常见的有自然语言法、列举法、描述法、韦恩(Venn)图法,以及后面将会学习的用“区间”表示集合。难点是描述法。
3、特定集合的表示
①非负整数集(或自然数集)--记作N;
②正整数集--记作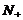 ,或
,或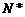 ;
;
③整数集--记作Z;
④有理数集--记作Q;
⑤实数集--记作R。
2、元素与集合的关系
元素与集合的关系有属于与不属于两种:元素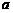 属于集合A,记作
属于集合A,记作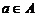 ;元素
;元素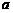 不属于集合A,记作
不属于集合A,记作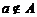 或
或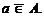
①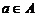 与
与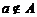 取决于
取决于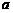 是不是集合A中的元素。根据集合中元素的确定性,可知对任何
是不是集合A中的元素。根据集合中元素的确定性,可知对任何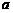 与A,在
与A,在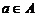 与
与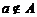 这两种情况中必有一种且只有一种成立。
这两种情况中必有一种且只有一种成立。
②符号“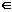 ”“
”“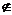 ”是表示元素与集合之间的关系的,不能用来表示集合与集合之间的关系
”是表示元素与集合之间的关系的,不能用来表示集合与集合之间的关系
1.集合的特性:确定性、互异性、无序性
4.例题思考:
例1:设U=R,A={x|-5<x<5},B={x|0≦x<7},求A∩B、A∪B、C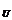 A 、C
A 、C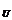 B、(C
B、(C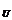 A)∩(C
A)∩(C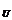 B)、(C
B)、(C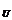 A)∪(C
A)∪(C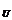 B)、C
B)、C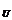 (A∪B)、C
(A∪B)、C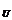 (A∩B)。
(A∩B)。
例2:全集U={x|x<10,x∈N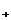 },A
},A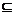 U,B
U,B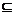 U,(C
U,(C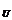 B)∩A={1,9},A∩B={3},C
B)∩A={1,9},A∩B={3},C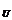 A)∩(C
A)∩(C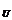 B)={4,6,7},求A、B。
B)={4,6,7},求A、B。
3.思考并回答以下问题:
(1) 试画出集合一节的知识结构图
(2) 什么叫交集、并集、补集?符号语言如何表示?图形语言?
(3) 交、并、补有何综合性质?
2.自学内容:通读教材_______页_______行至________页_______行,约用_______分钟。
1.学习目标:掌握集合、交集、并集、补集的有关性质,运行性质解决一些简单的问题,掌握集合的有关术语和符号。
例2.(1)如果定义在区间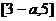 上的函数
上的函数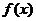 为奇函数,则
为奇函数,则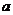 =_____
=_____
(2)已知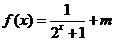 为奇函数,则
为奇函数,则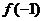 的值为
的值为
(3)函数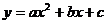 是偶函数的充要条件是___________
是偶函数的充要条件是___________
练习: (1)已知函数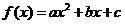 ,
,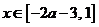 是偶函数,则
是偶函数,则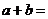
(2)定义在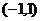 上的奇函数
上的奇函数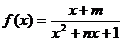 ,则常数
,则常数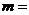 ____,
____,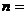 _____
_____
例3.(1)已知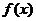 为
为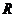 上的奇函数,当
上的奇函数,当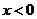 时,
时,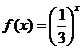 ,那么
,那么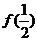 的值为
的值为
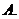
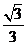
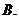
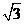
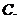
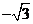
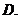
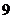
(2)设 >0时,
>0时,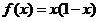 试问:当
试问:当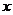 <0时,
<0时,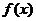 的表达式是什么?
的表达式是什么?
练习:已知函数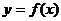 在R是奇函数,且当
在R是奇函数,且当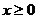 时,
时,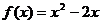 ,则
,则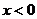 时,
时,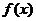 的解析式为_______________
的解析式为_______________

2.用图象
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com