
题目列表(包括答案和解析)
⒈设A={1,2,3,4,5},B={6,7,8},从集合A到集合B的映射中,满足f(1)≤f(2)≤f(3)≤f(4)≤f(5)的映射有( )
A.16个 B.14个 C.12个 D.8个
⒉已知映射f:A→B,其中集合A={-3,-2,-1,1,2,3,4},集合B中的元素是A中元素在映射f:A→B下的象,且对任意的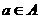 ,在B中和它对应元素是{
,在B中和它对应元素是{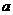 },则集合B中的
},则集合B中的
元素的个数是( )
A.4 B.5 C.6 D.7
3.用二分法求零点的近似值的步骤:
第1步:确定区间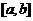 ,验证
,验证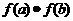 <0,给定精确度
<0,给定精确度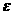 ;
;
第2步:求区间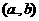 的中点
的中点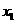 ;
;
第3步:计算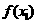 ;
;
(1)若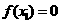 ,则
,则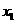 就是函数的零点;
就是函数的零点;
(2)若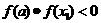 ,则令
,则令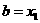 [此时零点
[此时零点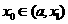 ];
];
(3)若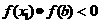 ,则令
,则令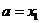 [此时零点
[此时零点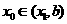 ].
].
第4步:判断是否达到精确度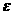 :即若
:即若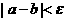 ,则得到零点近似值
,则得到零点近似值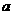 (或
(或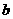 );否则重复(2)-(4)。
);否则重复(2)-(4)。
2.零点判断法
如果函数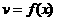 在区间
在区间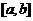 上的图象是连续不断的一条曲线,并且有
上的图象是连续不断的一条曲线,并且有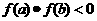 ,那么,函数
,那么,函数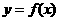 在区间
在区间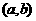 内有零点,即存在
内有零点,即存在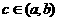 ,使得
,使得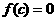 ,这个
,这个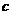 也就是方程
也就是方程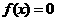 的根。
的根。
1.方程的根与函数的零点:方程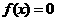 有实数根
有实数根 函数
函数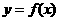 的图象与
的图象与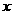 轴有交点
轴有交点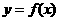 有零点.
有零点.
2.用函数与方程的思想解题
[例1]利用计算器,求方程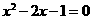 的一个近似解(精确到0.1).
的一个近似解(精确到0.1).
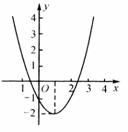
[解析]设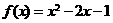 ,先画出函数图象的草图,如图的示.
,先画出函数图象的草图,如图的示.
因为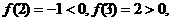
所以在区间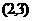 上,方程
上,方程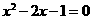 有一解,记为
有一解,记为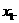
取2与3的平均数2.5
 因为
因为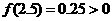 ,所以
,所以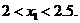
再取2与2.5的平均数2.25
因为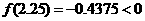 ,所以
,所以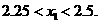
如此继续下去,得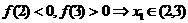
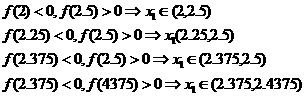
因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为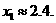
利用同样的方法,还可以求出方程的另一个近似解。
[点评]利用函数图象的性质求方程的根,这是因为若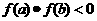 ,且
,且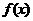 在
在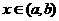 内单调,则必存在一个
内单调,则必存在一个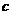 ,使
,使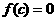 成立。
成立。
1.数形结合的思想
 数形结合的思想是本章重要的数学思想。
数形结合的思想是本章重要的数学思想。
[例1]某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量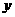 (件)与销售单价
(件)与销售单价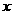 (元/件)可近似看作一次函数
(元/件)可近似看作一次函数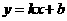 的关系(如图所示)。
的关系(如图所示)。
(1)根据图象,求一次函数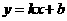 的表达式;(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元。①试用销售单价
的表达式;(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元。①试用销售单价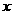 表示毛利润S;②试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
表示毛利润S;②试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
[解析](1)由图象知,当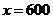 时,
时,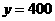 ;当
;当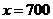 时,
时,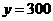 ,代入
,代入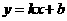 中,得
中,得
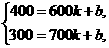 解得
解得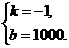
∴
(2)销售总价=销售单价×销售量=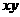 ,成本总价=成本单价×销售量=500
,成本总价=成本单价×销售量=500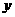 ,代入求毛利润的公式,得
,代入求毛利润的公式,得
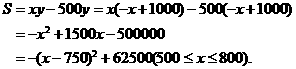
∴当销售单价为750元/件时,可获得最大毛利润62500元,此时销售量为250件。
[点评]数形结合有两类题型,一类是函数关系是由图形给出的,另一类是函数关系是一种定性的变化关系,反映在图形上又是怎样的要能正确判断。
6、分段函数问题;
[考题1]“依法纳税是每个公民应尽的义务”,国家征收个人工资、薪金所得税是分段计算的:总收入不超过1000元的,免征个人工资、薪金所得税;超过1000元部分需征税,设全月纳税所得额(所得额指工资、薪金中应纳税的部分)为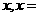 全月总收入-1000元,税率见下表:
全月总收入-1000元,税率见下表:
|
级数 |
全月应纳税所得额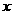 |
税率 |
|
1 |
不超过500元部分 |
5% |
|
2 |
超过500元至2000元部分 |
10% |
|
3 |
超过2000元至5000元部分 |
15% |
|
… |
… |
…45% |
|
9 |
超过100000元部分 |
|
(1)若应纳税额为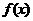 ,试用分段函数表示1-3级纳税额
,试用分段函数表示1-3级纳税额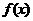 的计算公式.
的计算公式.
(2)某人2000年10月份工资总收入为4200元,试计算这个人10月份应纳个人所得税多少元?
[解析](1)依税率表,有
第一级: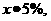
第二级: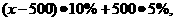
第三级:
即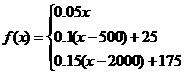
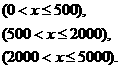
(2)这个人10月份纳税所得额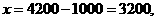
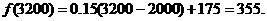
答:这个人10月份应缴纳个人所得税355元。
[点评]本题实际上是用表格形式给出的一个分段的一次函数,要注意这个分段函数中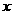 的不同取值范围.
的不同取值范围.
[考题2]某公司生产一种产品每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测知,市场对这种产品的年需求量为500件,且当出售的这种产品的数量为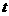 (单位:百件)时,销售所得的收入约为
(单位:百件)时,销售所得的收入约为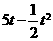 (万元).
(万元).
(1)若该公司的年产量为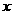 (单位:百件)
(单位:百件)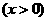 时,试把该公司生产并销售这种产品所得的年利润表示为当年产量
时,试把该公司生产并销售这种产品所得的年利润表示为当年产量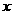 的函数.
的函数.
(2)当该公司的年产量多大时,当年所得利润最大?
[解析](1)当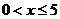 时,产品全部出售,当
时,产品全部出售,当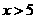 时,产品只能出售500件.
时,产品只能出售500件.
∴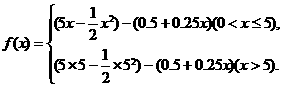
(2)当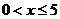 时,
时,
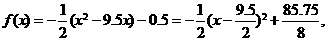
∴当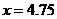 时,
时,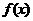 有最大值
有最大值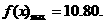
当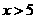 时,
时,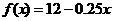 为单调减函数,∴
为单调减函数,∴
又∵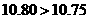 ,∴
,∴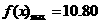 ,此时
,此时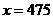 (件),
(件),
∴当年产量为475件时,利润最大.
[点评]求分段函数的最值和值域时,应先分段分别求其最值和值域,再以各段的最大值和最大者为函数的最大值,各段的最小值中最小者为函数的最小值;而各段的值域的并集则是函数的值域。
第三章 单元知识梳理与能力整合
5.比较函数模型的增长趋势
比较函数模型的增长趋势一般有两条途径:(1)不等式的方法,即作差比较或解不等式;(2)结合函数的图象,数形结合的方法。
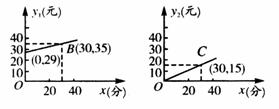
[例]为了发展电信事业方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“便民卡”和“如意卡”在某市范围内每月(30天)的通话时间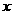 (分)与通话费
(分)与通话费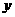 (元)的关系如图所示.
(元)的关系如图所示.
(1)分别求出通话费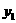 、
、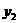 与通话时间
与通话时间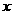 之间的函数关系式;
之间的函数关系式;
(2)请帮助用户计算,在一个月内使用哪种卡比较使用.
[分析]由图形可知,函数关系是线性关系,因此,可以用一次函数解决实际问题.
[解](1)由图象可设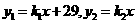 ,把点
,把点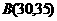 、
、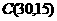 分别代入所设两函数式中得
分别代入所设两函数式中得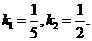
∴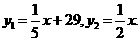
(2)令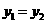 ,即
,即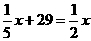 ,即
,即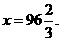
当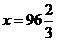 时,
时,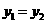 ,两种卡收费一致;
,两种卡收费一致;
当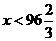 时,
时,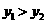 ,即“如意卡”便宜;
,即“如意卡”便宜;
当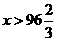 时,
时,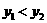 ,即“便民卡”便宜.
,即“便民卡”便宜.
[点评]使用哪种电话卡使用属于最优化问题,常借助于函数的图象、函数的最值去解决.
4.数学模型为对数函数的问题
形如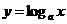 (
(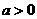 且
且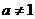 )的函数叫做对数函数,
)的函数叫做对数函数,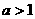 时,此函数为增函数;
时,此函数为增函数;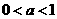 时,此函数为减函数,虽然直接以对数函数作为模型的应用问题不是很多,但我们知道,对数运算实际是求指数的运算,因此在指数函数模型中,也常用对数计算。
时,此函数为减函数,虽然直接以对数函数作为模型的应用问题不是很多,但我们知道,对数运算实际是求指数的运算,因此在指数函数模型中,也常用对数计算。
[例]在不考虑空气阻力的条件下,火箭的最大速度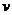 (m/s)和燃料的质量
(m/s)和燃料的质量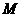 (kg)、火箭(除燃料外)的质量
(kg)、火箭(除燃料外)的质量 (kg)的关系
(kg)的关系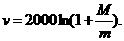 当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?
当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?
[解]由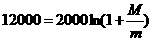 ,即
,即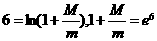 ,利用计算器算得
,利用计算器算得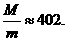
[例]某城市现有人口100万,如果20年后该城市人口总数不超过120万,年自然增长率应控制在多少以内?
[解]设年自然增长率为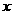 ,依题意有:
,依题意有:
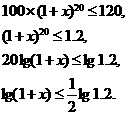
由计算器计算得 %。
%。
答:年自然增长率应控制在0.9%以内。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com