
题目列表(包括答案和解析)
4、已知点C在线段AB的延长线上,且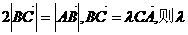 等于 (
)
等于 (
)
A.3 B.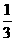 C.
C.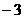 D.
D.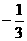
3、△OAB中,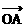 =
=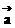 ,
,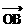 =
=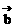 ,
,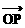 =
=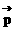 ,若
,若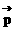 =
=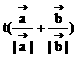 ,t∈R,则点P在 ( )
,t∈R,则点P在 ( )
A、∠AOB平分线所在直线上 B、线段AB中垂线上
C、AB边所在直线上 D、AB边的中线上
2、已知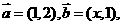 且
且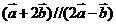 ,则
,则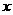 的值为
( )
的值为
( )

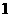
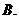
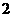

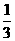
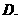
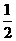
1、若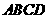 为正方形,
为正方形,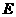 是
是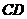 的中点,且
的中点,且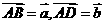 ,则
,则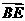 =
( )
=
( )

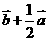
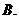
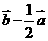

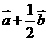
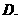
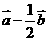
3、已知 、
、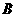 、
、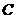 三点的坐标分别为
三点的坐标分别为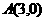 、
、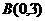 、
、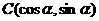 ,
,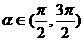 ,
,
(1)若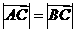 ,求角
,求角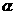 的值;
的值;
(2)若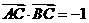 ,求
,求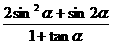 的值。
的值。
2、已知向量 = (
= (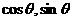 )和
)和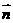 =(
=(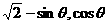 ),
), 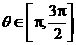 .
.
(1)求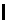
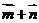
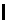 的最大值;
的最大值;
(2)若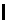
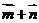
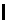 =
=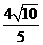 ,求
,求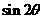 的值.
的值.
1、平面向量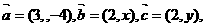 已知
已知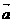 ∥
∥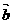 ,
,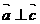 ,求
,求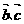 及
及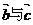 夹角。
夹角。
2.重要定理、公式
(1)向量共线定理:如果有一个实数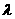 使
使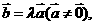 那么
那么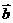 与
与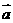 是共线向量;反之,如果
是共线向量;反之,如果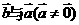 是共线向量,那么有且只有一个实数
是共线向量,那么有且只有一个实数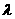 ,使
,使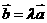 。
。
(2)平面向量基本定理;如果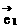 ,
,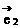 是同一平面内的两个不共线向量,那么对于该平面内任一向量
是同一平面内的两个不共线向量,那么对于该平面内任一向量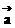 ,有且只有一对数数λ1,λ2,满足
,有且只有一对数数λ1,λ2,满足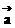 =λ1
=λ1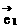 +λ2
+λ2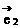 。
。
(3)两个向量平行
:设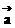 =(x1,y1),
=(x1,y1),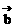 =(x2,y2),则
=(x2,y2),则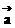 ∥
∥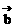

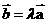
 x1y2-x2y1=0
x1y2-x2y1=0
(4)两个向量垂直:设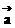 =(x1,y1),
=(x1,y1), 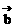 =(x2,y2),则
=(x2,y2),则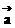 ⊥
⊥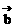

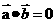
 x1x2+y1y2=0
x1x2+y1y2=0
(5)线段定比分点公式: 设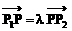 , 则
, 则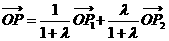
设P(x,y),P1(x1,y1),P2(x2,y2),则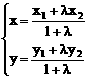
1.向量的三种线性运算及运算的三种形式。
向量的加减法,实数与向量的乘积,两个向量的数量积都称为向量的线性运算,前两者的结果是向量,两个向量数量积的结果是数量。每一种运算都可以有三种表现形式:图形、符号、坐标语言。主要内容列表如下:
|
运 算 |
图形语言 |
符号语言 |
坐标语言 |
|
加法与减法 |
 |
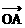 + +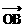 = =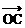 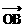 - -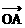 = =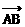 |
记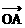 =(x1,y1), =(x1,y1),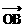 =(x1,y2) =(x1,y2)则 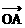 + +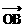 =(x1+x2,y1+y2) =(x1+x2,y1+y2)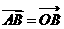 - -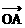 =(x2-x1,y2-y1) =(x2-x1,y2-y1) |
 |
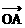 + +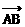 = =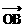 |
|
|
|
实数与向量 的乘积 |
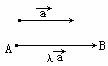 |
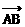 =λ =λ λ∈R |
记 =(x,y) =(x,y)则λ  =(λx,λy) =(λx,λy) |
|
两个向量 的数量积 |
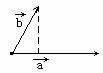 |
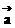 · ·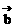 =| =|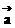 || ||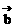 | |cos< 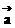 , ,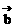 > > |
记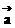 =(x1,y1), =(x1,y1), 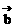 =(x2,y2) =(x2,y2)则 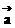 · ·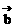 =x1x2+y1y2 =x1x2+y1y2 |
3.二次函数的图象的顶点坐标为(1,2),且过(0,0)点,则函数解析式为_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com