
题目列表(包括答案和解析)
(三)解答题
11.确定函数y=x+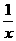 (x>0)的单调区间,并用定义证明.
(x>0)的单调区间,并用定义证明.
12.设f(x)是定义在R上的增函数,f(xy)=f(x)+f(y),f(3)=1,求解不等式f(x)+f(x-2)>1.
13.求函数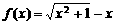 在区间
在区间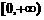 上的最大值.
上的最大值.
14.求函数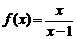 在
在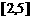 上的最大值和最小值.
上的最大值和最小值.
(二)填空题
8.函数y=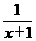 的单调区间为___________.
的单调区间为___________.
9.函数f(x)=2 x2-3|x|的单调减区间是___________.
10.已知函数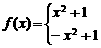
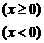 的单调递增区间是 。
的单调递增区间是 。
(一)选择题
1.下列函数中,在区间(0,2)上为增函数的是( )
A.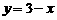 B.
B.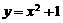 C.
C.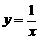 D.
D.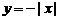
2.已知函数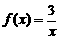 ,则下列区间不是递减区间的是( )
,则下列区间不是递减区间的是( )
A.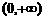 B.
B.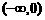 C.
C. D.
D.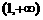
3.设函数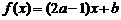 是
是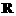 上的减函数,则有( )
上的减函数,则有( )
A.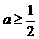 B.
B.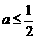 C.
C.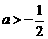 D.
D.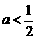
4.函数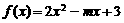 ,当
,当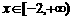 时为增函数,
时为增函数,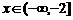 时为减函数,则
时为减函数,则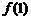 等于( )
等于( )
A.-3 B.13 C.7 D.由m而定
5.已知 是
是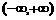 上的减函数,若
上的减函数,若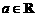 ,则( )
,则( )
A.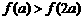 B.
B.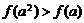
C.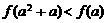 D.
D.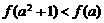
6.函数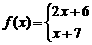
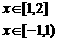 ,则
,则 的最大值与最小值分别为( )
的最大值与最小值分别为( )
A.10,6 B.10,8 C.8,6 D.以上都不对
7.函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则a的范围是( )
A.a≥5 B.a≥3 C.a≤3 D.a≤-5
[考题1]二次函数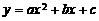 的单调性如何?
的单调性如何?
[解析]由二次函数的图象可知:
(1)当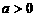 时,二次函数
时,二次函数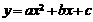 在
在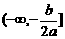 上递减,在
上递减,在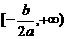 上递增;
上递增;
(2)当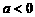 时,二次函数
时,二次函数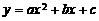 在
在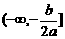 上递增,在
上递增,在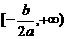 上递减。
上递减。
[点评]同样可以知道:一次函数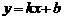 ,反比例函数
,反比例函数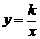 的单调性为:当
的单调性为:当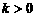 时,函数
时,函数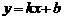 在R上递增,函数
在R上递增,函数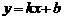 在R上递减,函数
在R上递减,函数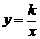 在
在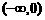 和
和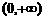 上递增。
上递增。
[考题2]求下列函数的增区间与减区间。
 (1)
(1)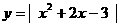 ;(2)
;(2)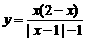 .
.
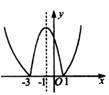
[解析](1)令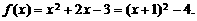 先做出
先做出 的图象,保留其在
的图象,保留其在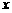 轴及
轴及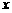 轴上方,就得到
轴上方,就得到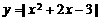 的图象,如图所示。由图象易得:
的图象,如图所示。由图象易得:
递增区间是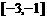 和
和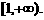
递减区间是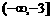 和
和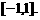
(2)当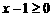 且
且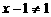 时,得
时,得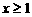 且
且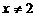 ,函数
,函数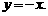
当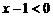 且
且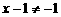 时,
时,
得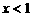 且
且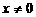 时,函数
时,函数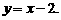
∴增区间是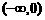 和
和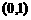 ;减区间是
;减区间是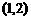 和
和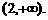
[点评]利用函数图象确定函数的单调区间,具体做法是:先化简函数式,然后再画出它的草图,最后根据函数定义域与草图的位置、状态,确定函数的单调区间。
[考题3](1)求函数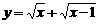 的最小值;
的最小值;
(2)已知 ,对于函数
,对于函数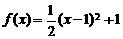 ,若
,若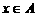 时,
时,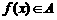 ,求
,求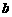 的值。
的值。
[解析](1)由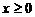 ,且
,且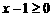 得,函数的定义域为
得,函数的定义域为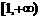 .而函数
.而函数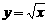 和
和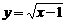 在
在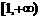 上都是增函数。则得
上都是增函数。则得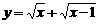 也是增函数,当
也是增函数,当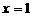 时,它取得最小值,所以
时,它取得最小值,所以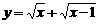 的最小值为1。
的最小值为1。
(2)函数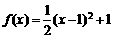 表示开口向上,顶点坐标是
表示开口向上,顶点坐标是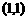 ,对称轴是
,对称轴是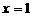 的抛物线。
的抛物线。
因此,当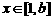 时,
时, 是增函数。
是增函数。
∴当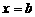 时,
时, 取最大值
取最大值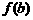 ,而
,而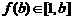 ,
,
故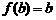 ,即
,即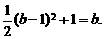
整理得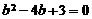 ,解得
,解得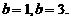
∵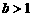 ,∴
,∴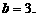
[点评]有关二次函数的问题,要特别注意二次函数的对称轴是否在给定的区间上?应该截取二次函数图象的哪一部分?从而解决问题。
[考题4](1)证明函数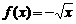 在定义域上是减函数。
在定义域上是减函数。
(2)证明函数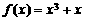 在R上是增函数。
在R上是增函数。
[解析](1)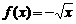 的定义域为
的定义域为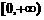 ,设
,设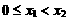 ,则
,则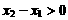 ,且
,且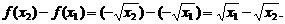
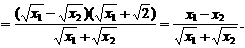
∵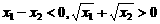 ,
,
∴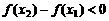 ,即
,即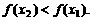
∴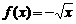 在它的定义域
在它的定义域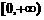 上是减函数。
上是减函数。
(2)设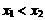 ,则
,则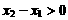 ,
,
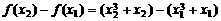
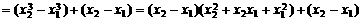
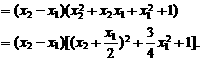
∵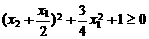 ,∴
,∴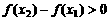 ,
,
即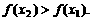 ∴
∴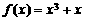 在R上是增函数。
在R上是增函数。
[点评]在“作差变形”的过程中,我们昼化成几个最简因式的乘积,也可以把其中的因式化成几个完全平方式的和形式,这也是值得学习的解题技巧,在判断因式的正负号时,经常采用这种方法。
[例5]已知函数 的定义域为R,且满足
的定义域为R,且满足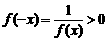 ,且
,且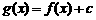 *(
*(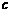 为常数)在区间
为常数)在区间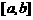 上是减函数,判断并证明
上是减函数,判断并证明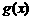 在区间
在区间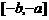 上的单调性。
上的单调性。
[分析]从所求结果入手,设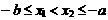 ,只要再判断
,只要再判断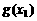 与
与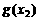 的大小即可。
的大小即可。
[解]设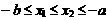 ,
,
则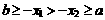 ,∵
,∵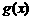 在区间
在区间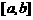 上是减函数,
上是减函数,
∴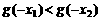 ,即
,即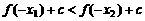 ,
,
则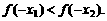 又∵
又∵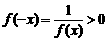 ,
,
∴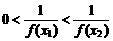 ,即
,即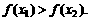
∴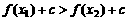 ,即
,即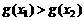 ,
,
∴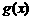 在区间
在区间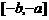 上是减函数。
上是减函数。
[考题6]已知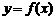 在定义域
在定义域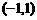 上是减函数,且
上是减函数,且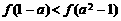 ,求
,求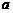 的取值范围。
的取值范围。
[分析]充分利用单调性构造关于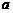 的不等式,同时注意定义域的限制。
的不等式,同时注意定义域的限制。
[解析]由题意可知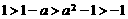 ,
,
即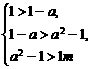 解得
解得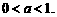
[点评](1)对于抽象函数一类问题的考查着重在基本的性质和理论知识上,有时亦可举出满足条件的特例函数来帮助解答或寻找思路。(2)要注意化归和转化的数学思想的应用。
3.函数的最大(小)值
(1)函数最大值的定义
对于最大值定义的理解
①M首先是一个函数值,它是值域的一个元素。如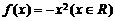 的最大值为0,有
的最大值为0,有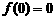 ,注意对(1)②中存在一词的理解;
,注意对(1)②中存在一词的理解;
②对于定义域内全部元素,都有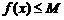 成立,“任意”是说对每一个值都必须满足不等式;
成立,“任意”是说对每一个值都必须满足不等式;
③这两条缺一不可,若只有(1)①,M不是最大值,如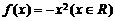 ,对任意
,对任意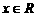 ,都有
,都有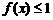 成立,但1不是最大值;否则大于零的任意实数都是最大值了;最大值的核心就是不等式
成立,但1不是最大值;否则大于零的任意实数都是最大值了;最大值的核心就是不等式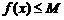 ,故不能只有(1)①;
,故不能只有(1)①;
④若将(1)中的“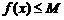 ”改为“
”改为“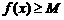 ”,则需将最大值定义中的“最大值”改为“最小值”。这就是函数
”,则需将最大值定义中的“最大值”改为“最小值”。这就是函数 的最小值的定义。
的最小值的定义。
2.单调性与单调区间
(1)这个区间可以是整个定义域。
(2)这个区间也可以是定义域的真子集。
(3)有的函数不具有单调性。
如函数 的定义域为R,但不具有单调性;再如
的定义域为R,但不具有单调性;再如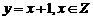 ,它的定义域不是区间,也不能说它在定义域上具有单调性。
,它的定义域不是区间,也不能说它在定义域上具有单调性。
函数单调性的常用判断方法
(1)图象法:先作出函数图象,利用图象直观判断函数的单调性。
(2)直接法:就是对于我们所熟悉的函数,如一次函数、二次函数、反比例函数等,直接写出它们的单调区间。
[注意]当单调递增(或递减)区间由几个区间组成时,一般情况下不能取它们的并集,而应该用“和”或“,”连接。
1.增函数和减函数
证明函数的单调性其步骤为:
(1)取值:设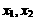 为该区间内任意的两个值,且
为该区间内任意的两个值,且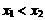 ;
;
(2)作差变形:作差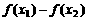 ,并通过因式分解、配方、有理化等方法,向有利于判断差值符号的方式变形;
,并通过因式分解、配方、有理化等方法,向有利于判断差值符号的方式变形;
(3)定号:确定最值的符号,当符号不确定时,可考虑分类讨论。
(4)判断:根据定义作出结论。
[注意]在用定义法证明不等式时,为了确定符号,一般是将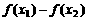 尽量分解出
尽量分解出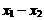 因式,再将剩下的因式化成积商的形式,或化成几个非负实数的和等,这样有利于该因式的符号的确定。
因式,再将剩下的因式化成积商的形式,或化成几个非负实数的和等,这样有利于该因式的符号的确定。
11、定义在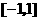 上的函数
上的函数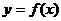 是减函数,且是奇函数,若
是减函数,且是奇函数,若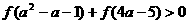 ,求实数
,求实数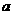 的范围.
的范围.
12﹡、设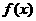 是定义在
是定义在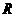 上的偶函数,其图象关于直线
上的偶函数,其图象关于直线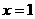 对称,对任意
对称,对任意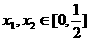 ,都有
,都有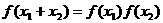 . (I)设
. (I)设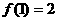 ,求
,求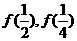 ; (II)证明
; (II)证明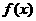 是周期函数.
是周期函数.
10、已知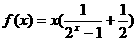 ,(1)判断
,(1)判断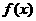 的奇偶性;(2)证明:
的奇偶性;(2)证明: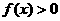
9、判断下列函数的奇偶性
1)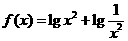 2)
2)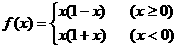
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com