
题目列表(包括答案和解析)
1、举生活中单值对应的实例。
经过前阶段的学习,我们知道函数是建立在两个非空数集之间的单值对应,其实,生活中还有很多在两个集合之间建立单值对应的例子。
如:班级里的每一位学生都有唯一确定的座号与他对应。
上述事例是函数吗?若不是,我们如何定义该类对应?
2、会判断一个对应是否是映射,理解映射与函数的关系。
学习重点:
映射的概念
学习过程:
1、了解映射的概念,会借助图形理解映射的概念。
4、已知函数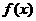 对一切实数
对一切实数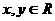 都有
都有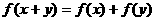 ,且当
,且当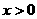 时,
时,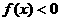 ,又
,又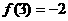 。
。
(1)试判定该函数的奇偶性;(2)试判断该函数在R上的单调性;(3)求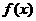 在[
在[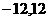 ]上的最大值和最小值。
]上的最大值和最小值。
高一年级数学导学提纲
§2.1.4 映射的概念
执笔人:王玉红 审核人:纪尧兵
学习目标:
3、函数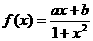 是定义在
是定义在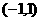 上的奇函数,且
上的奇函数,且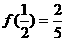 。
。
(1)求函数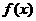 的解析式;(2)用函数单调性定义证明
的解析式;(2)用函数单调性定义证明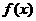 在(
在(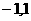 )上是增函数;
)上是增函数;
(3)解不等式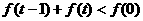 。
。
2、定义在[-2,2]上的偶函数g(x),当x≥o时,g(x)单调递减,若g(1-m)<g(m)成立,求m的取值范围。
1、已知函数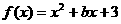 ,
,
(1)若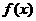 在区间
在区间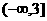 上为减函数,在
上为减函数,在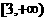 上为增函数,求b的值及
上为增函数,求b的值及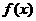 在
在
[4,6]上的值域;
(2)若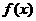 在区间
在区间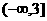 上为减函数,求b的取值范围;
上为减函数,求b的取值范围;
(3)若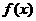 在区间[0,1]上有最小值3,求b的值。
在区间[0,1]上有最小值3,求b的值。
6、已知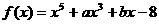 ,且
,且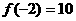 ,则
,则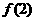 的值为
的值为
5、若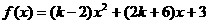 是偶函数,则
是偶函数,则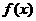 单调递增区间为
单调递增区间为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com