
题目列表(包括答案和解析)
17. (本小题满分12分)
已知圆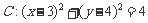 ,(Ⅰ)若直线
,(Ⅰ)若直线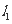 过定点
过定点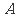 (1,0),且与圆
(1,0),且与圆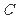 相切,求
相切,求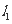 的方程; (Ⅱ) 若圆
的方程; (Ⅱ) 若圆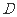 的半径为3,圆心在直线
的半径为3,圆心在直线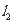 :
: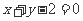 上,且与圆
上,且与圆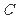 外切,求圆
外切,求圆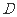 的方程.
的方程.
解:(Ⅰ)①若直线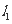 的斜率不存在,即直线是
的斜率不存在,即直线是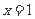 ,符合题意. …………………2分
,符合题意. …………………2分
②若直线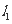 斜率存在,设直线
斜率存在,设直线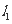 为
为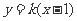 ,即
,即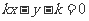 .
.
 由题意知,圆心(3,4)到已知直线
由题意知,圆心(3,4)到已知直线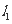 的距离等于半径2,即
的距离等于半径2,即 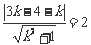 ……4分
……4分
解之得 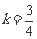 .…………………………………5分
.…………………………………5分
所求直线方程是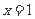 ,
,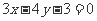 . …………………………………… 6分
. …………………………………… 6分
(Ⅱ)依题意设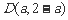 ,……………… 7分
,……………… 7分
又已知圆的圆心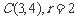 , 由两圆外切,可知
, 由两圆外切,可知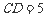
∴可知  =
=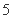 , ……………………………………… 9分
, ……………………………………… 9分
解得 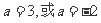 , ∴
, ∴ 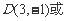
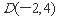 ,
,
∴ 所求圆的方程为 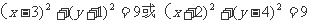 .…… 12分
.…… 12分
B卷(共50分)
16. (本小题满分12分)
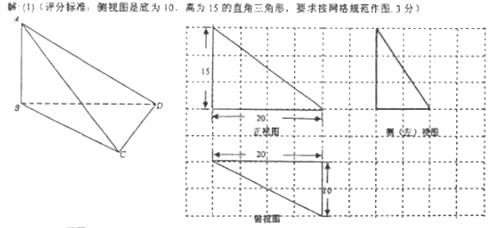
如图,在三棱锥A-BCD中,AB⊥平面BCD,它的正视图和俯视图都是直角三角形,图中尺寸单位为cm。(I)在正视图右边的网格内,按网格尺寸和画三视图的要求,画出三棱锥的侧(左)视图;(II)证明:CD⊥平面ABD;(III)按照图中给出的尺寸,求三棱锥A-BCD的侧面积。

11.__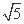 _______. 12. (-2,1)
.
13._
_______. 12. (-2,1)
.
13._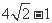 __. 14.
__. 14. 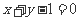 .
.
24.(本小题满分12分)
已知以点C (t, )(t∈R , t ≠ 0)为圆心的圆与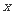 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
厦门理工学院附中(杏南中学)
2010-2011 学年 下 学期 4 月 数学 学科 高一 年段阶段测试卷
考试时间: 120分钟 总分: 150分 命题:陈文娴 审核: 万龙兰
A卷(共100分)
23.(本大题满分12分)
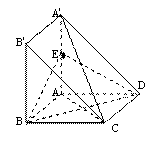 如图,四边形
如图,四边形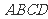 与
与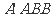 都是边长为
都是边长为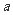 的正方形,点E是
的正方形,点E是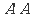 的中点,
的中点,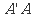 ⊥平面ABCD.
⊥平面ABCD.
(I)计算:多面体A'B'BAC的体积;
(II)求证: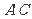
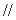 平面BDE;
平面BDE;
(Ⅲ) 求证:平面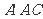 ⊥平面BDE.
⊥平面BDE.
22.(本小题满分10分)
有一座圆弧形拱桥,它的跨度为60米,拱高为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,有一次洪水来袭,拱顶离水面只有4米,是否采取紧急措施?
21.已知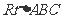 的两直角边长分别为
的两直角边长分别为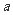 、
、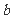 ,斜边长为
,斜边长为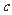 ,则直线
,则直线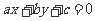 与圆
与圆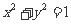 的位置关系是
。
的位置关系是
。
20. 已知点A(x,5)关于点(1,y)的对称点(-2,-3),则点P(x,y)到原点的距离是 。
19.已知点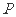 在圆
在圆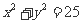 上移动,
上移动,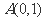 则
则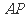 的中点
的中点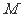 的轨迹方程是
的轨迹方程是
18. 直线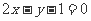 被圆
被圆 所截得的弦长为
所截得的弦长为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com