
题目列表(包括答案和解析)
20.(本小题满分16分)
设z是虚数,ω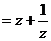 是实数,且-1<ω<2.
是实数,且-1<ω<2.
(1)求 |z| 的值及z的实部的取值范围;
(2)设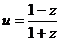 ,求证:u为纯虚数;
,求证:u为纯虚数;
(3)求ω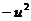 的最小值.
的最小值.
数学试题(附加题)
19.(本小题满分16分)
若不等式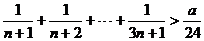 对一切正整数
对一切正整数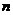 都成立,求正整数
都成立,求正整数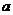 的最大值,并用数学归纳法证明你的结论.
的最大值,并用数学归纳法证明你的结论.
18.(本小题满分16分)
若某一等差数列的首项为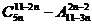 ,公差为
,公差为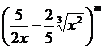 展开式中的常数项,其中m是7777-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
展开式中的常数项,其中m是7777-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
17.(本小题满分14分)
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为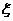 ,求随机变量
,求随机变量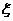 的期望
的期望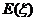 .
.
16.(本小题满分14分)
设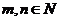 ,
,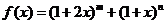 .
.
(Ⅰ)当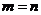 =2011时,记
=2011时,记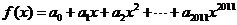 ,
,
求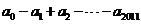 ;
;
(Ⅱ)若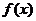 展开式中
展开式中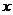 的系数是20,则当
的系数是20,则当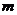 、
、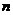 变化时,试求
变化时,试求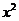 系数的最小值.
系数的最小值.
15.(本小题满分14分)
男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛.
(1)若选出男运动员3名,女运动员2名,有多少种不同的选派方法?
(2)若队长至少有1人参加,有多少种不同的选派方法?
(3)若至少有1名女运动员,有多少种不同的选派方法?
(4)若既要有队长, 又要有女运动员,有多少种不同的选派方法?
22、(本题满分12分)
解:⑴∵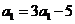 ∴
∴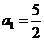
⑵∵ ∴
∴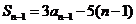 (
(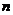 ≥2)∴
≥2)∴
∴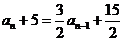
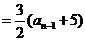 ∴
∴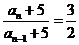 (为常数) (
(为常数) (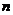 ≥2)
≥2)
∴数列 是以
是以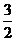 为公比的等比数列∴
为公比的等比数列∴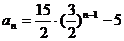
⑶∵ ,
,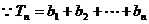 ,则
,则
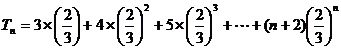 ①
①
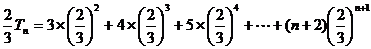 ②
②
用错位相减法①-②得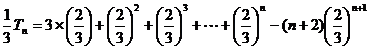
得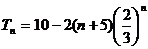 ,
,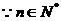 所以
所以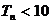

21、(本题满分12分)证明:①设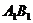 的中点为
的中点为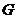 ,连结
,连结 、
、 ,
,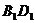
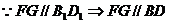 ,又
,又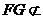 面
面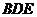 而
而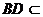 面
面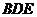 ,所以
,所以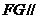 面
面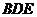
同理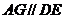 ,
, 面
面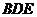 ,
,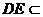 面
面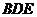 所以
所以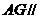 面
面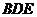 ,又因为
,又因为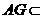 面
面
 面
面 ,
,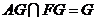
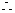 面
面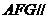 面
面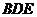 ,而
,而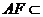 面
面
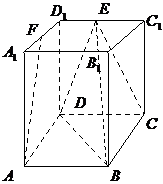 所以
所以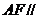 面
面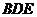
②在长方体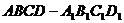 中,
中,
由条件得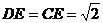 ,则
,则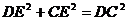 ,
,
所以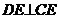 ,又
,又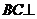 面
面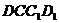 ,
,
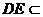 面
面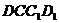 所以
所以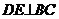 ,而
,而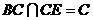 ,
,
同时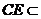 面
面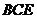 ,
,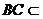 面
面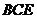 ,所以
,所以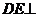 面
面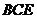
20、(本题满分12分)解:分别设长、宽为 、
、 ;水池的总造价为
;水池的总造价为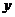 元,
元,
则有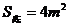
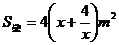
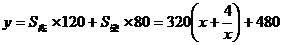
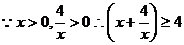 得
得
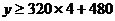 ,即
,即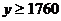 (元)
(元)
当且仅当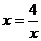 时,即当且仅当
时,即当且仅当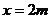 时,总造价
时,总造价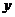 最小为1760元
最小为1760元
答:当池底的长和宽分别造为2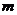 的正方形时,总造价最低为1760元
的正方形时,总造价最低为1760元
备注:用其它方法可以相应给分
19、(本题满分12分)解:①如图
②由图可知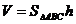 ,又
,又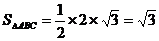
所以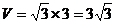
③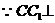 面
面 ,所以
,所以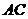 即为直线
即为直线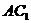 在平面
在平面 内的射影,故直线
内的射影,故直线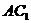 与平面
与平面
 所成的角为
所成的角为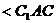 ,在
,在 中,因为
中,因为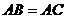 ,
,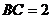 ,而由视图可知三角形的高是
,而由视图可知三角形的高是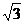 ,所以
,所以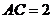 ,由②得
,由②得 ,所以
,所以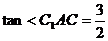
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com