
题目列表(包括答案和解析)
4、分别过点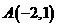 和点
和点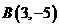 的两条直线均垂直于
的两条直线均垂直于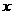 轴,则这条直线间的距离为____________
轴,则这条直线间的距离为____________
3、直线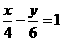 与
与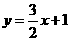 之间的距离是______________
之间的距离是______________
2、点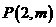 到直线
到直线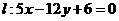 的距离为
的距离为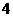 ,则
,则 =
( )
=
( )
A.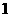 B.
B.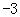 C.
C.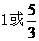 D.
D.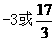
1、点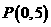 到直线
到直线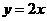 的距离是
( )
的距离是
( )
A.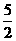 B.
B.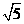 C.
C.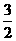 D.
D.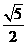
22.解:设容器底面积短边长为xm,则另一边长为(x+0.5)m,高为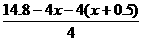 =3.2-2x.由3.2-2x>0和x>0得0<x<1.6,设容器的容积为vm3,则有V=x(x+0.5)(3.2-2x) (0<x<1.6)即:V=-2x3+2.2x2+1.6x.∴V/=-6x2+4.4x+1.6.令V/=0得-6x2+4.4x+1.6=0 即x1=1,x2=-
=3.2-2x.由3.2-2x>0和x>0得0<x<1.6,设容器的容积为vm3,则有V=x(x+0.5)(3.2-2x) (0<x<1.6)即:V=-2x3+2.2x2+1.6x.∴V/=-6x2+4.4x+1.6.令V/=0得-6x2+4.4x+1.6=0 即x1=1,x2=-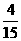 (舍去).∴在(0,1.6)内只有x=1处使V/=0.由题意,若x过小(接近0)或过大(接近1.6)时,V很小(接近0),因此,当x=1时y取得最大值.
y大=-2+2.2+1.6=1.8,这时高为3.2-2×1=1.2
(舍去).∴在(0,1.6)内只有x=1处使V/=0.由题意,若x过小(接近0)或过大(接近1.6)时,V很小(接近0),因此,当x=1时y取得最大值.
y大=-2+2.2+1.6=1.8,这时高为3.2-2×1=1.2
答:容器的高为1.2m时容积最大,最大容积为1.8m3.

 2004-2005学年度第二学期期中考试
2004-2005学年度第二学期期中考试
22.用总长14.8m的钢条制做一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积的最大?并求出他的最大容积.
14.解:直线方程为y=-x+4,联立方程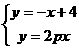 ,消去y得,
,消去y得,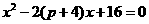 .
.
设A(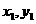 ),B(
),B(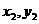 ),得
),得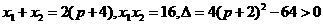
所以: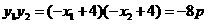 ,p>0.
,p>0.
由已知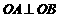 可得
可得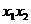 +
+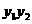 =0,从而16-8p=0,得p=2.
=0,从而16-8p=0,得p=2.
所以抛物线方程为y2=4x,焦点坐标为F(1,0).
14.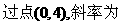 -1的直线与抛物线
-1的直线与抛物线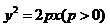 交于两点A,B,如果
交于两点A,B,如果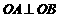 (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。
17.解:(1)令f/(x)=3x2-x-2 >0,得x<-
>0,得x<- 或x>1.
或x>1.
∴函数的单调增区间为(-∞,-  )、(1,+∞),单调减区间为(-
)、(1,+∞),单调减区间为(- ,1)
,1)
(2)原命题等价于f/(x)在[-1,2]的最大值小于m.由f/(x)=0,得x= - 或1,又f(-1)=
或1,又f(-1)=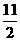 ,f(-
,f(- )=5
)=5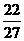 ,f(1)=
,f(1)=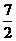 ,f(2)=7
,f(2)=7
∴m>[f(x)]max=7.
17.设f(x)=x3- x2-2x+5
x2-2x+5
(1)求函数f(x)的单调递增,递减区间:
(2)当x∈[-1,2]时,f(x)<m恒成立,求实数m的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com