23、某人忘记了电话号码的最后一个数字，因而他随意地拨号，假设拨过了的号码不再重复，试求下列事件的概率：

　 (1)第3次拨号才接通电话；

　 (2)拨号不超过3次而接通电话.

解：设A₁={第i次拨号接通电话}，i=1，2，3.

(1)第3次才接通电话可表示为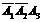于是所求概率为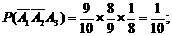

(2)拨号不超过3次而接通电话可表示为：A₁+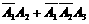于是所求概率为

　 P(A₁+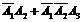)=P(A₁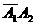)+P()+P()=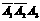

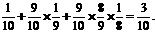
22、高三(1)班、高三(2)每班已选出3名学生组成代表队，进行乒乓球对抗赛，比赛规则是：

①按“单打、双打、单打”顺序进行三盘比赛；

②代表队中每名队员至少参加一盘比赛，不得参加两盘单打比赛；

③先胜两盘的队获胜，比赛结束.

已知每盘比赛双方胜出的概率均为

(Ⅰ)根据比赛规则，高三(1)班代表队共可排出多少种不同的出场阵容？

(Ⅱ)高三(1)班代表队连胜两盘的概率是多少？

(Ⅲ)高三(1)班代表队至少胜一盘的概率为多少？

解：(Ⅰ)参加单打的队员有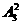种方法.参加双打的队员有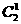种方法.　　 (2分)

所以，高三(1)班出场画容共有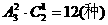　 (4分)

(Ⅱ)高三(1)班代表队连胜两盘，可分为第一盘、第二盘胜或第一盘负，其余两盘胜.(6分)

所以，连胜两盘的概率为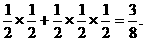　 (8分)

(Ⅲ)高三(1)班至少胜一盘，可分为：

(1)胜一盘，此时的概率为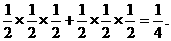　 (9分)

(2)胜两盘，此时的概率为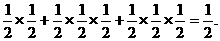　 (11分)

所以，高三(1)班至少胜一盘的概率为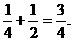　 (12分)

或：高三(1)班代表队至少胜一盘的对立事件为输掉前两盘所以，

所求概率为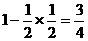(12分)

21、在袋里装30个小球，其中彩球有：n个红色、5个蓝色、10个黄色，其余为白球.

求：①如果已经从中取定了5个黄球和3个蓝球，并将它们编上了不同的号码后排成一排，那么使蓝色小球互不相邻的排法有多少种？

②如果从袋里取出3个都是相同颜色彩球(无白色)的概率是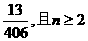，计算红球有几个？

③根据②的结论，计算从袋中任取3个小球至少有一个是红球的概率？

解：①将5个黄球排成一排只有种排法，将3个蓝球放在5个黄球所形成的6个空上，有种放法 ∴所求的排法为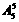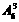=5×4×3×2×6×5×4=14400(种)…4分

②取3个球的种数为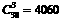 设“3个球全红色”为事件A，“3个全蓝色”为事件B，“3个球全黄色”为事件C.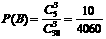 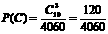　　∵A、B、C为互斥事件　 ∴P(A+B+C)= P(A)+P(B)+P(C)　 即 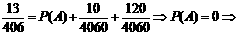取3个球红球的个数≤2，又∵n≥2，故n = 2 ……8分 ③记“3个球中至少有一个是红球”为事件D，则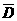为“3个球中没有红球” 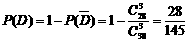或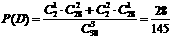　

20、有甲、乙两个篮球运动员，甲投篮的命中率为0.7，乙投篮的命中率为0.6，每人各投篮三

　　 次：

　 (Ⅰ)甲恰有2次投中的概率；　

　 (Ⅱ)乙至少有1次投中的概率；

　 (Ⅲ)甲、乙两人投中数相等的概率。

解：(Ⅰ)甲恰有2次投中的概率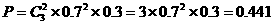;…3分

(Ⅱ)乙至少有1次投中的概率可视为3次独立重复试验中乙投中次数不少于1的事件发生的概率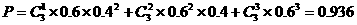……7分

　(Ⅲ)分4种情况①甲乙均未投中;②甲乙均投中1次;③甲乙均投中2次;④甲乙均投中3次;故所求概率为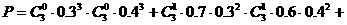

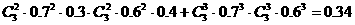.…………12分

19、有外形相同的球分装在三个不同的盒子中，每个盒子10个球，其中第一个盒子中7个球标有字母A，3个球标有字母B；第二个盒子中有红球和白球各5个；第三个盒子中有红球8个，白球2个，试验按如下规则进行：先在第一个盒子中任取一球，若取得标有字母A的球，则在第二个盒子中任取一球；若第一次取得标有字母B的球，则在第三个盒子中任取一球，如果第二次取出的是红球，则称试验成功，求试验成功的概率

解：设事件A{从第一个盒子中取得一个标有字母A的球}，事件B={从第一个盒子中取

得一个标有字母B的球}，

则A，B互斥，且P(A)=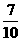，P(B)=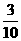；(4分)

事件C={从第二号盒子中取一个红球}，

事件D={从第三号盒子中取一个红球}，

则C，D互斥，且P(C)=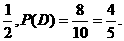(8分)显然，事件A·C与事件B·D互斥，且事件A与C是相互独立的， B与D也是相互独立的.所以试验成功的概率为

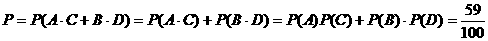(11分)

答：本次试验成功的概率为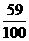

18、排球比赛的规则是5盘3胜制，A、B两队每盘比赛获胜的概率都相等且分别为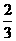和.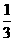

(Ⅰ)前2盘中B队以2:0领先，求最后A、B队各自获胜的概率;

　　 (Ⅱ)B队以3:2获胜的概率.

解:(Ⅰ)设最后A获胜的概率为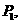设最后B获胜的概率为

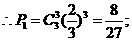　　　　　　　　　　　　　 …………………………………4分

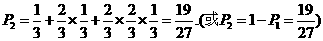　　　　　 ……………………8分

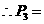
(Ⅱ)设B队以3:2获胜的概率为　　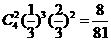　 ……………………12

17、某班数学兴趣小组有男生和女生各3名，现从中任选2名学生去参加校数学竞赛，求：

(I)恰有一名参赛学生是男生的概率；

(II)至少有一名参赛学生是男生的概率；

(Ⅲ)至多有一名参赛学生是男生的概率。

解、基本事件的种数为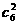=15种　 )

(Ⅰ)恰有一名参赛学生是男生的基本事件有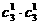=9种 这一事件的概率P₁=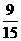=0.6(5分)

(Ⅱ)至少有一名参赛学生是男生这一事件是由两类事件构成的，即恰有一名参赛学生是男生和两名参赛学生都是男生所求事件的概率P₂=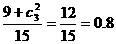　　 ……(9分)

(Ⅲ)至多有一名参赛学生是男生这一事件也是由两类事件构成的，即参赛学生没有男生和恰有一名参赛学生是男生所求事件的概率P₃=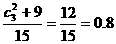

16、猎人射击距离100米远处的静止目标命中的概率为0.6

(1)如果猎人射击距离100米远处的静止目标3次，求至少有一次命中的概率；

(2)如果猎人射击距离100米远处的动物，假如第一次未命中，则进行第二次射击，但由于枪声惊动动物使动物逃跑从而使第二次射击时动物离猎人的距离变为150米，假如第二次仍未命中，则必须进行第三次射击，而第三次射击时动物离猎人的距离为200米。假如击中的概率与距离成反比，。求猎人最多射击三次命中动物的概率。

解：(1)记事件“猎人射击距离100米远处的静止目标3次，至少有一次命中”为A事件，

则P(A)=1-P(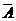)=1-0.4×0.4×0.4=0.936.

　 (2)记事件“第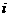次击中动物”为事件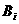( 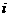=1,2,3)，记事件“最多射击3次而击中动物”为事件B.

由条件P(B₁)=0.6, P(B₁)=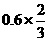=0.4, P(B₁)=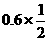=0.3,

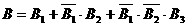　∵,且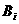是相互独立事件,又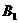、、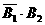是互斥事件，

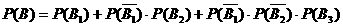∴=0.832.

15、某产品检验员检查每一件产品时，将正品错误地鉴定为次品概率为0.1，将次品错误地鉴定为正品的概率为0.2，如果这位检验员要鉴定4件产品，这4件产品中3件是正品，1件是次品，试求检验员鉴定成正品，次品各2件的概率。

解：将3件正品，1件次品鉴定为2件正品，2件次品有两种可能：

　 (1)将原1件次品仍鉴定为次品，原3件正品中有1件错误地鉴定为次品，这时的概率为。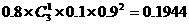

　 (2)将原1件次品鉴定为正品，再将3件正品中的2件错误地鉴定为次品，这时的概率为。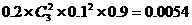

于是所求的概率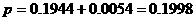

14、一盒中装有20个大小相同的弹子球，其中红球10个，白球6个，黄球　　 4个，一小孩随手拿出4个，求至少有3个红球的概率

解：恰有3个红球的概率P₁= 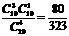　……4′

有4个红球的概率P₂=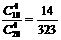……8′

至少有3个红球的概率P=P₁+P₂=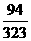…………12′