
题目列表(包括答案和解析)
15, (满分8分)
设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为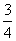 ,遇
,遇
到红灯(禁止通行)的概率为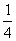 ,假定汽车只在遇到红灯或到达目的地才停止前进,
,假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求:
(1)  的概率分布列 (5)
的概率分布列 (5)
(2) 停车时最多已通过3个路口的概率 (3分)
16, (满分9分)
(1)有3名男生,2名女生排成一排:若男生甲不站排头,女生乙不站在排尾,则有多少种不同的排法?(3分)
(2)
已知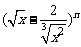 展开式中偶数项的二项式系数之和为256,求含
展开式中偶数项的二项式系数之和为256,求含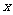 项的系数.(3分)
项的系数.(3分)
(3) 求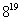 除以9的余数?
除以9的余数?
 |
2 |
4 |
5 |
6 |
8 |
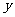 |
30 |
40 |
50 |
60 |
70 |
17, (9分)某种产品的广告费支出
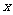 与销售额
与销售额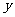 之间有如右图对应数据:
之间有如右图对应数据:
(单位:百万元)
(1)画出散点图;(3分)
(2)求线性回归方程;(4分)
(参考公式: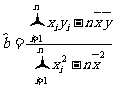 ,
,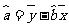 )
)
(3)预测当广告费支出为7百万元时的销售额。(2分)
18, (满分9分) 由下列各式:
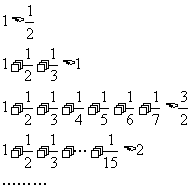
(1) 由上述所给的式子, 归纳出一般性的结论, (3分) (归纳错误不给分)
(2) 用数学归纳法证明你所归纳的结论 (6分)
19, (满分9分)
(1) (3分)已知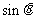 与
与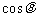 的等差中项是
的等差中项是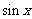 ,等比中项是
,等比中项是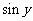 .
.
试用综合法证明: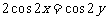 ;(3分) (不用综合法证明不给分)
;(3分) (不用综合法证明不给分)
(2)已知函数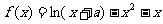 在
在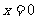 处取得极值 (6分)
处取得极值 (6分)
①求实数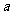 的值; (2分)
的值; (2分)
②若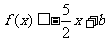 时
时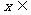
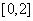 恒成立,求实数b的取值范围;(4分)
恒成立,求实数b的取值范围;(4分)

 高二下期中考数学(理)试卷
高二下期中考数学(理)试卷
22.(本小题满分10分)已知椭圆的中心为坐标原点O,其中一个焦点坐标为(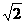 ,0),离心率为
,0),离心率为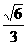 .
.
(1)求椭圆C的方程;
(2)已知向量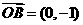 ,是否存在斜率为
,是否存在斜率为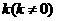 的直线l,l与曲线C相交于M、N两点,使向量
的直线l,l与曲线C相交于M、N两点,使向量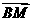 与向量
与向量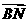 的夹角为
的夹角为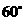 ,且
,且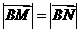 ? 若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
? 若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
21.(本小题满分10分)已知动点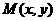 与定点
与定点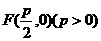 和定直线
和定直线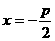 的距离相等.
的距离相等.
(1)求动点M的轨迹C的方程;
(2)设M、N是轨迹C上异于原点O的两个不同点,直线OM和ON的倾斜角分别为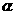 和
和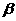 ,当
,当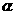 、
、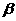 变化,且
变化,且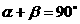 时. 求证:直线MN恒过一定点.
时. 求证:直线MN恒过一定点.
20.(本小题满分10分)如图,点P是矩形ABCD所在的平面外一点, E、F分别是AB、PC的中点.
(1)求证:EF∥平面PAD;
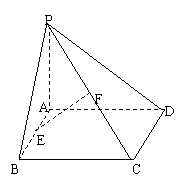 (2)若PA⊥平面ABCD,且PA=AD,求证:EF⊥平面PCD.
(2)若PA⊥平面ABCD,且PA=AD,求证:EF⊥平面PCD.
19.(本小题满分10分)点P为双曲线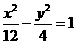 的渐近线与右准线在第一象限内的交点,圆C与双曲线的两条渐近线都相切,且P为切点,求圆C的标准方程.
的渐近线与右准线在第一象限内的交点,圆C与双曲线的两条渐近线都相切,且P为切点,求圆C的标准方程.
18.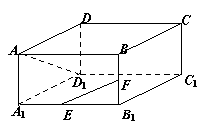 (本小题满分8分)长方体
(本小题满分8分)长方体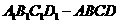 中,
中,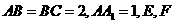 分别是
分别是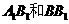 的中点,
的中点,
求: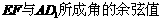 .
.
17.(本小题满分8分)已知直线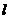 与直线
与直线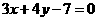 的倾斜角相等,并且与两坐标轴围成的三角形的面积等于24,求直线
的倾斜角相等,并且与两坐标轴围成的三角形的面积等于24,求直线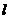 的方程.
的方程.
16.下面有四个命题:
①经过空间一点与两条异面直线都相交的直线有且只有一条;
②经过空间一点与两条异面直线都垂直的直线有且只有一条;
③经过空间一点与两条异面直线都平行的平面有且只有一个;
④经过空间一点与两条异面直线都垂直的平面有且只有一个.
其中真命题的序号是_______________(把符合要求的命题序号都填上).
15.函数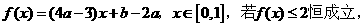 则
则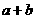 的最大值为 ;
的最大值为 ;
14.已知双曲线的虚轴长是实轴长与焦距的等比中项,则此双曲线的离心率是 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com