
题目列表(包括答案和解析)
3.空间四边形的对角线互相垂直且相等,顺次连结这个空间四边形各边的中点,所组成的
四边形是 ( )
A.正方形 B.矩形 C.平行四边形 D.梯形
2.如果直线 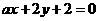 与直线
与直线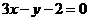 平行, 那么实数a等于 ( )
平行, 那么实数a等于 ( )
A.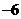 B.
B. 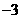 C.
C.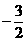 D.
D.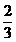
1.不等式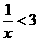 等价于
( )
等价于
( )
A.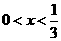 B.
B.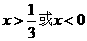 C.
C.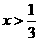 D.
D.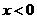
得 分 评卷人 (19)(本小题满分10分)
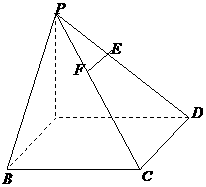 已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=
已知ABCD是正方形,PA⊥平面ABCD,且PA=AB=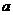 ,E、F是侧棱PD、PC上的点,且
,E、F是侧棱PD、PC上的点,且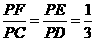 .
.
(1)求证:EF∥平面PAB ;
(2)求直线PC与底面ABCD所成角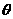 的正切值;
的正切值;

得 分 评卷人 (20)(本小题满分12分)
已知直线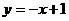 与椭圆
与椭圆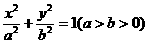 相交于
相交于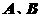 两点.
两点.
(1)若椭圆的离心率为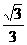 ,焦距为2,求线段
,焦距为2,求线段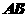 的长;
的长;
(2)在(1)的椭圆中,设椭圆的左焦点为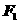 ,求△
,求△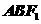 的面积。
的面积。
高二数学试卷第4页(共6页)

得 分 评卷人 (21)(本小题满分12分)


 如图,四棱锥
如图,四棱锥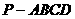 中,
中,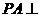 底面
底面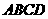 ,
,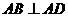 ,
,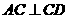 ,
,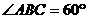 ,
,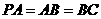 ,
,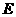 是
是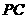 的中点.
的中点.
(1)求证: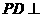 面
面 ;
;
(2)求二面角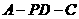 的平面角的正弦值.
的平面角的正弦值.
高二数学试卷第5页(共6页)

得 分 评卷人 (22)(本小题满分12分)

 已知椭圆
已知椭圆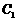 的方程是
的方程是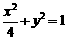 ,双曲线
,双曲线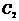 的左、右焦点分别是
的左、右焦点分别是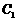 的左、右顶点,双曲线
的左、右顶点,双曲线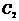 的左、右顶点分别是
的左、右顶点分别是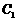 的左、右焦点.
的左、右焦点.
(1)求双曲线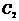 的方程;
的方程;
(2)若直线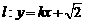 与双曲线
与双曲线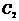 有两个不同的交点
有两个不同的交点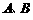 ,且
,且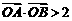 (
(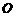 为原点),求实数
为原点),求实数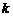 的取值范围.
的取值范围.
高二数学试卷第6页(共6页)
(13)已知某球的体积与其表面积的数值相等,则此球体的体积为 ______________.
(14)方程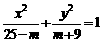 表示焦点在y轴上的椭圆,则m的取值范围是 .
表示焦点在y轴上的椭圆,则m的取值范围是 .
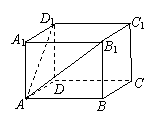 (15)如图,长方体
(15)如图,长方体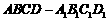 中,
中,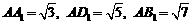 ,
,
则长方体的对角线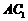 长等于 ________.
长等于 ________.
(16)以双曲线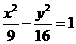 的右焦点为圆心,且与其渐近线相切的圆的方程是_______________.
的右焦点为圆心,且与其渐近线相切的圆的方程是_______________.
(17)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
(18)经过抛物线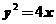 的焦点
的焦点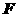 作与对称轴垂直的直线, 交抛物线于
作与对称轴垂直的直线, 交抛物线于 、
、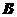 两点,
两点, 是抛物线的顶点,再将直角坐标平面沿
是抛物线的顶点,再将直角坐标平面沿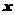 轴折成直二面角, 此时∠
轴折成直二面角, 此时∠ 的余弦值是
.
的余弦值是
.
高二数学试卷第3页(共6页)
四个选项中,只有一项是符合题目要求的.)
(1)垂直于同一条直线的两条直线一定 ( )
A.平行 B.相交 C.异面 D.以上都有可能
(2)“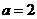 ”是“直线
”是“直线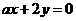 平行于直线
平行于直线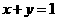 ”的
( )
”的
( )
A.充分必要条件 B.必要而不充分条件
C.充分而不必要条件 D.既不充分也不必要条件
(3)一个平行于棱锥底面的截面与棱锥的底面的面积之比为1∶9,则截面把棱锥的高分成两段的长度之比为 ( )
A. B. C. D.
(4)空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是 ( )
A.垂直且相交 B.垂直但不相交
C.相等但不一定垂直 D.不相等也不垂直
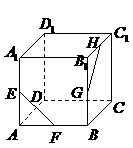 (5)如图,在正方体
(5)如图,在正方体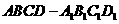 中,
中,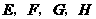 分别为
分别为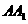 ,
,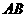 ,
,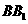 ,
,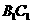 的中点,则异面直线
的中点,则异面直线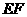 与
与 所成的角等于( )
所成的角等于( )
A.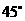 B.
B.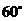 C.
C. D.
D.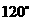
(6)若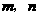 是两条不同的直线,
是两条不同的直线,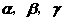 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )
A.若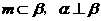 ,则
,则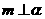 B.若
B.若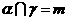
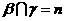 ,
,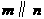 ,则
,则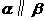
C.若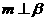 ,
,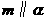 ,则
,则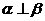 D.若
D.若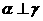 ,
,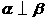 ,则
,则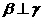
高二数学试卷第1页(共6页)
(7)一动圆的圆心在抛物线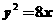 上,且动圆恒与直线
上,且动圆恒与直线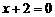 相切,则此动圆必过定点( )
相切,则此动圆必过定点( )
A.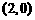 B.
B.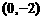 C.
C.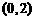 D.
D.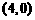
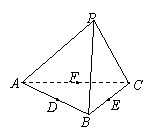
(8)如图,在正四面体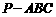 中,
中,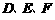 分别是
分别是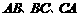 的中点,
的中点,
则下列四个结论中不成立的是( )
A.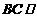 平面
平面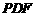 B.
B.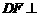 平面
平面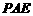
C.平面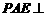 平面
平面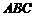 D.平面
D.平面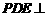 平面
平面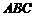
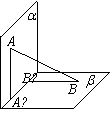 (9)如图,平面a⊥平面b,A∈a,B∈b,AB与两平面a,b 所成的角
(9)如图,平面a⊥平面b,A∈a,B∈b,AB与两平面a,b 所成的角
分别为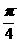 和
和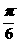 ,过A,B分别作两平面交线的垂线,垂足为A¢,B¢,
,过A,B分别作两平面交线的垂线,垂足为A¢,B¢,
则AB∶A¢B¢=( )
A.4∶3 B.3∶2 C.2∶1 D.3∶1
(10)半径为1的球面上的四点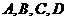 是正四面体的顶点,则
是正四面体的顶点,则 与
与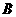 两点间的球面距离为
( )
两点间的球面距离为
( )
A.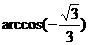 B.
B.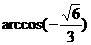 C.
C.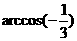 D.
D.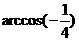
(11)设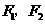 分别是双曲线
分别是双曲线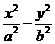 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点 ,使
,使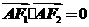 且
且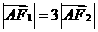 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A.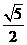 B.
B.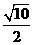 C.
C.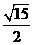 D.
D.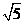
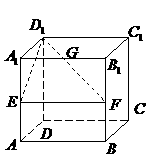
(12)在棱长为1的正方体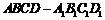 中,
中,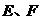 分别为棱
分别为棱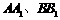 的中点,
的中点,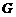 为棱
为棱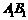 上的一点,且
上的一点,且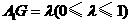 .则点
.则点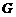 到平面
到平面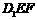 的距离为( )
的距离为( )
A.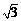 B.
B.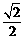 C.
C.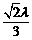 D.
D.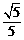
高二数学试卷第2页(共6页)
数 学 试 题
命题人:昆明第三中学 徐青华
第II卷(非选择题共64分)
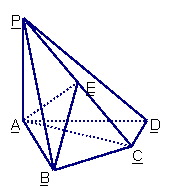
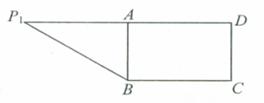
22.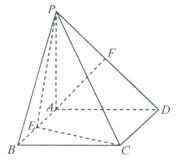 (本题满分14分)在直角梯形P1DCB中,P1D∥BC,
(本题满分14分)在直角梯形P1DCB中,P1D∥BC,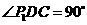 且
且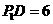 ,
,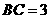 ,
,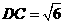 ,A是
,A是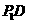 的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PB的中点。
的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角,设E、F分别是线段AB、PB的中点。
(1)求证:AF∥平面PEC;
(2)求PD与平面ABCD所成角的大小;
(3)求点D到平面PEC的距离。
21.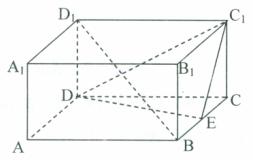 (本题满分12分)如图,ABCD--A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点,
(本题满分12分)如图,ABCD--A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点,
(1)求异面直线AC1和DE所成角的大小;
(2)求异面直线AC1和DE的距离。
20.(本题满分12分)C64分子是与C60分子类似的球状多面体结构,它有64个顶点,以每个顶点为一端点都有3条棱,各面是四边形或六边形,求C64分子中四边形和六边形的个数。
19.(本题满分12分)10人中有7人会说英语,6人会说德语(每人至少会其中一种),现要选出6人去完成一项任务,要求3人会说英语,3人会说德语,求有多少种选法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com