
题目列表(包括答案和解析)
12.已知P是椭圆上的一点,F1、F2是椭圆的两个焦点,∠PF1F2=90°,∠PF2F1=30°,则椭圆的离心率是__________.
解析:因为e=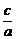 =
=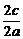 =
=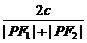 ,
,
于是在△PF1F2中,由正弦定理知e=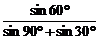 =
=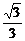 .
.
答案: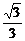
11.若椭圆的两个焦点为F1(-4,0)、F2(4,0),椭圆的弦AB过点F1,且△ABF2的周长为20,那么该椭圆的方程为__________.
解析:△ABF2的周长:|AF2|+|AF1|+|BF2|+|BF1|=2a+2a=4a=20,
∴a=5.又∵c=4,∴b=3.
∴椭圆的方程为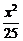 +
+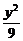 =1.
=1.
答案: 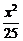 +
+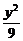 =1
=1
10.已知F1、F2为椭圆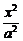 +
+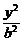 =1(a>b>0)的焦点,M为椭圆上一点,MF1垂直于x轴,且∠F1MF2=60°,则椭圆的离心率为
=1(a>b>0)的焦点,M为椭圆上一点,MF1垂直于x轴,且∠F1MF2=60°,则椭圆的离心率为
A.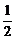 B.
B.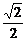
C.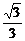 D.
D.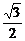
分析:本题考查如何求椭圆的离心率.
解:∵MF1⊥x轴,∴M点的横坐标为xM=-c.把xM代入椭圆方程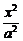 +
+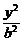 =1中,得yM=
=1中,得yM=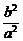 ,如下图所示.
,如下图所示.
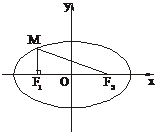
在Rt△MF1F2中,tan∠F1MF2=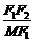 =
=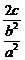 =
=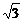 ,
,
即2ac=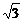 b2.∴
b2.∴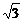 a2-2ac-
a2-2ac-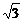 c2=0.
c2=0.
每一项都除以a2,得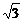 -2e-
-2e-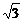 e2=0,
e2=0,
解得e1=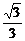 或e2=-
或e2=-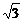 (舍).
(舍).
答案:C
第Ⅱ卷(非选择题 共70分)
9.若椭圆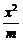 +
+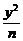 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线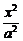 -
-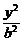 =1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
=1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
A.m-a B.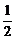 (m-a)
(m-a)
C.m2-a2 D.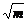 -
-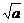
解析:|PF1|+|PF2|=2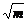 ,|PF1|-|PF2|=2
,|PF1|-|PF2|=2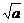 ,
,
∴|PF1|=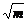 +
+ 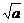 ,|PF2|=
,|PF2|=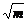 -
-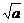 .
.
∴|PF1|·|PF2|=m-a.
答案:A
8.方程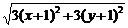 =|x+y-2|表示的曲线是
=|x+y-2|表示的曲线是
A.椭圆 B.双曲线
C.抛物线 D.不能确定
解析:数形结合法.动点P(x,y)到定点(-1,-1)和定直线x+y-2=0距离之比为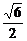 .
.
答案:B
7.已知双曲线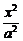 -
-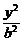 =1和椭圆
=1和椭圆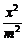 +
+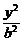 =1(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边的三角形是
=1(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边的三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
解析:双曲线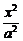 -
-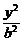 =1的离心率e1=
=1的离心率e1=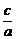 =
=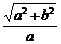 ,
,
椭圆的离心率e2=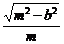 .
.
∵e1与e2互为倒数,∴e1e2=1,
即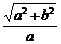 ·
·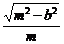 =1,整理得a2+b2=m2.
=1,整理得a2+b2=m2.
∴以a、b、m为边的三角形是直角三角形.
答案:B
6.以椭圆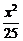 +
+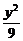 =1的焦点为焦点,离心率e=2的双曲线方程是
=1的焦点为焦点,离心率e=2的双曲线方程是
A.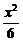 -
-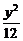 =1 B.
=1 B.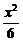 -
-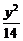 =1
=1
C.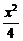 -
-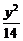 =1 D.
=1 D.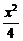 -
-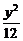 =1
=1
解析:a2=25,b2=9,则c2=16,c=4,椭圆焦点坐标为(4,0)、(-4,0).
双曲线的焦点仍为(4,0)、(-4,0),由于e=2,c=4,
∴a=2,b2=c2-a2=12.
∴双曲线方程为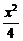 -
-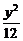 =1.
=1.
答案:D
5.双曲线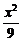 -
-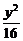 =1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为
=1的两焦点为F1、F2,点P在双曲线上,且直线PF1、PF2倾斜角之差为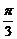 ,则△PF1F2的面积为
,则△PF1F2的面积为
A.16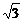 B.32
B.32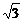
C.32 D.42
解析:由题意可知|PF1|-|PF2|=6,∠F1PF2=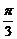 ,|F1F2|=10.
,|F1F2|=10.
由余弦定理,得|F1F2|2=(|PF1|-|PF2|)2+|PF1|·|PF2|,
∴|PF1|·|PF2|=64.
∴S=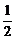 ×64sin
×64sin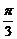 =16
=16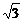 ,选A.
,选A.
答案:A
4.若双曲线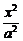 -
-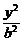 =1的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率是
=1的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率是
A.2 B.3
C.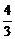 D.
D.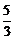
解析:由2b=a+c得4b2=a2+2ac+c2,
即3c2-2ac-5a2=0,∴3e2-2e-5=0.∴e=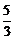 .
.
答案:D
3.已知点M在椭圆上,椭圆方程为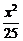 +
+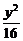 =1,M点到左准线的距离为2.5,则它到右焦点的距离为
=1,M点到左准线的距离为2.5,则它到右焦点的距离为
A.7.5 B.12.5
C.2.5 D.8.5
解析:∵a=5,b=4,∴c=3.
两准线间的距离为2·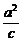 =2×
=2×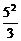 =
=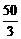 .
.
M到左准线的距离为2.5,则M到右准线的距离为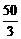 -2.5=
-2.5=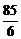 .
.
设椭圆右焦点为F,
则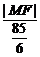 =
=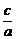 =
=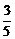 ,∴|MF|=8.5.
,∴|MF|=8.5.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com