
题目列表(包括答案和解析)
6.设k>1,则关于x,y的方程(1-k) x2+ y 2=k2-1所表示的曲线是 ( )
A.长轴在y轴上的椭圆 B.长轴在x轴上的椭圆
C.实轴在y轴上的双曲线 D.实轴在x轴上的双曲线
5.与椭圆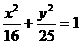 共焦点,且两准线间的距离为
共焦点,且两准线间的距离为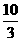 的双曲线方程为 ( )
的双曲线方程为 ( )
A.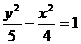 B.
B.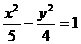
C.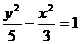 D.
D.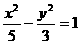
4.连接双曲线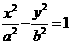 与
与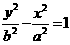 的四个顶点构成的四边形的面积为S1,连接它们的的四个焦点构成的四边形的面积为S2,则S1:S2的最大值是 ( )
的四个顶点构成的四边形的面积为S1,连接它们的的四个焦点构成的四边形的面积为S2,则S1:S2的最大值是 ( )
A.2 B. 1 C.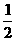 D.
D.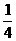
3.已知椭圆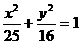 上一点P到椭圆一个焦点的距离为3,则P到另一个焦点的距离为
上一点P到椭圆一个焦点的距离为3,则P到另一个焦点的距离为
( )
A.2 B.3 C.5 D.7
2.椭圆短轴长是2,长轴是短轴的2倍,则椭圆中心到准线距离是 ( )
A.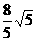 B.
B.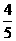
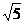 C.
C. D.
D.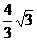
1.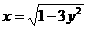 所表示的曲线是 ( )
所表示的曲线是 ( )
A.双曲线 B.椭圆
C.双曲线的一部分 D.椭圆的一部分
19.如图,AB,CD是两条异面直线,AB=CD=3a,E,F分别是线段AD,BC上的点,且ED=2AE,FC=2BF,EF=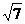 a,G∈BD,EG∥AB.
a,G∈BD,EG∥AB.
(1)求AB与CD所成的角;
(2)求△EFG的面积.
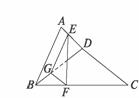
解:(1)∵ED=2AE,EG∥AB,∴DG=2BG.
∵FC=2BF,∴FG∥DC.
∴∠EGF即为AB与CD所成的角或其补角.
∵AB=CD=3a,EG=2a,GF=a,又EF=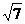 a,
a,
∴cos∠EGF=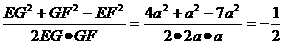 .
.
∴∠EGF=120°.∴AB与CD所成的角为60°.
(2)S△EFG=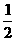 EG·GF·sin120°
EG·GF·sin120°
=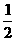 ×2a×a×sin120°
×2a×a×sin120°
= a2.
a2.
18.如图所示,今有一正方体木料ABCD-A1B1C1D1,其中M,N分别是AB,CB的中点,要过D1,M,N三点将木料锯开,请你帮助木工师傅想办法,怎样画线才能顺利完成?
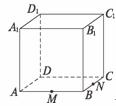
解:作法如下:
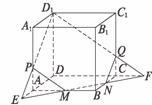
(1)连结MN并延长交DC的延长线于F,连结D1F交CC1于Q,连结QN;
(2)延长NM交DA的延长线于E,连结D1E交A1A于P,连结MP;
(3)依次在正方体各个面上画线D1P,PM,MN,NQ,QD1,即为木工师傅所要画的线.
17.如图,a,b,c为不共面的三条直线,且相交于一点O,点M,N,P分别在直线a,b,c上,点Q是b上异于N的点,判断MN与PQ的位置关系,并予以证明.
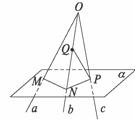
证法一:(反证法)
假设MN与PQ共面于β,则点M,N,P,Q∈β.
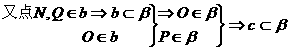
同理,a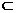 β.
β.
∴a,b,c共面,与已知a,b,c不共面矛盾.故MN与PQ为异面直线.
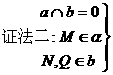
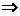

点Q MN,
MN,
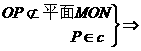 点P
点P 平面MON.
平面MON.
故平面MON内一点Q与平面外一点P的连线PQ与平面内不过Q点的直线MN是异面直线.
16.如图,E、F、G、H分别是空间四边形ABCD各边上的点,且有AE∶EB=AH∶HD=m,CF∶FB=CG∶GD=n.
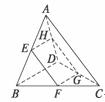
(1)证明E、F、G、H四点共面.
(2)m、n满足什么条件时,EFGH是平行四边形?
(3)在(2)的条件下,若AC⊥BD,试证明EG=FH.
(1)证明:
∵AE∶EB=AH∶HD,∴EH∥BD.
∵CF∶FB=CG∶GD,
∴FG∥BD.∴EH∥FG.∴E、F、G、H四点共面.
(2)解:当且仅当EH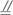 FG时,四边形EFGH为平行四边形.
FG时,四边形EFGH为平行四边形.
∵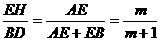 ,∴EH=
,∴EH=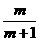 BD.
BD.
同理,FG=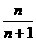 BD.由EH=FG得m=n.
BD.由EH=FG得m=n.
故当m=n时,四边形EFGH为平行四边形.
(3)证明:当m=n时,AE∶EB=CF∶FB,∴EF∥AC.
又∵AC⊥BD,∴∠FEH是AC与BD所成的角.∴∠FEH=90°.
从而EFGH为矩形,∴EG=FH.
点评:空间四边形是立体几何的一个基本图形,它各边中点的连线构成平行四边形;当两对角线相等时该平行四边形为菱形;当两对角线互相垂直时,该平行四边形为矩形;当两对角线相等且互相垂直时,该平行四边形为正方形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com