
题目列表(包括答案和解析)
6、已知三棱锥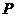 -
-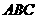 的四个顶点均在半径为1的球面上,且满足
的四个顶点均在半径为1的球面上,且满足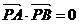 ,
,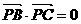 ,
,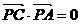 ,则三棱锥
,则三棱锥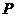 -
-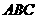 的侧面积的最大值为( )
的侧面积的最大值为( )
A.1
B.2 C.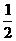 D.
D.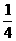
5、 已知动点P(x、y)满足10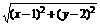 =|3x+4y+2|,则动点P的轨迹是( )
=|3x+4y+2|,则动点P的轨迹是( )
A.椭圆 B.双曲线 C.抛物线 D.无法确定
4、已知点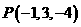 ,且该点在三个坐标平面
,且该点在三个坐标平面 平面,
平面,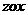 平面,
平面, 平面上的射影的坐标依次为
平面上的射影的坐标依次为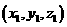 ,
,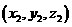 和
和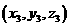 ,则( )
,则( )
A、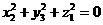 B、
B、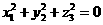 C、
C、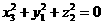 D、以上结论都不对
D、以上结论都不对
3、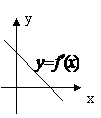 函数
函数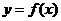 的图象过原点且它的导函数
的图象过原点且它的导函数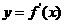 的图象是
的图象是
如图所示的一条直线, 则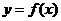 的图象的顶点在( )
的图象的顶点在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2、已知点P在椭圆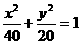 上,
上, 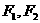 是椭圆的两个焦点,
是椭圆的两个焦点,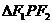 是直角三角形,则这样的点P有( )
是直角三角形,则这样的点P有( )
A.2个
B.4个
C.6个
D.8个
1.在下列命题中:①若a、b共线,则a、b所在的直线平行;②若a、b所在的直线是异面直线,则a、b一定不共面;③若a、b、c三向量两两共面,则a、b、c三向量一定也共面;④已知三向量a、b、c,则空间任意一个向量p总可以唯一表示为p=xa+yb+zc.其中正确命题的个数为( )
A.0
B.1
C.2
D.3
20、数列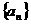 的各项均为正数,
的各项均为正数,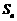 为其前
为其前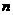 项和,对于任意
项和,对于任意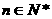 ,总有
,总有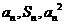 成等差数列.
成等差数列.
(1)求数列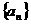 的通项公式;(2)设数列
的通项公式;(2)设数列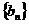 的前
的前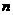 项和为
项和为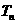 ,且
,且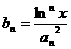 ,求证:对任意实数
,求证:对任意实数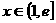 (
(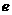 是常数,
是常数,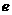 =2.71828
=2.71828 )和任意正整数
)和任意正整数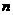 ,总有
,总有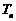
 2;
2;
(3) 正数数列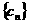 中,
中,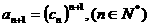 .求数列
.求数列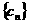 中的最大项.
中的最大项.
19、(本题10分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆 元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获 元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为
元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为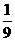 ,
,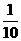 ,
,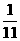 ,且各车是否发生事故相互独立,求一年内该单位在此保险中:
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额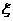 的分布列与期望.
的分布列与期望.
18、(本题10分)(1)在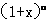 的展开式中,若第
的展开式中,若第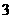 项与第
项与第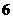 项系数相等,且
项系数相等,且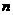 等于多少?
等于多少?
(2)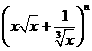 的展开式奇数项的二项式系数之和为
的展开式奇数项的二项式系数之和为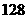 ,求展开式中二项式系数最大的项
,求展开式中二项式系数最大的项
17. (本题8分)已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com