
题目列表(包括答案和解析)
19.已知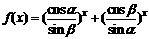 ,其中
,其中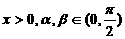 (1)证明:若
(1)证明:若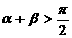 ,则
,则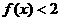
(2)试问(1)的逆命题是否成立?若成立给予证明,若不成立说明理由或给出反例.
18. 设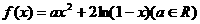 ,(1)若
,(1)若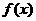 在
在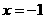 处有极值,求a;
处有极值,求a;
(2)若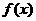 在
在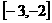 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
17.设关于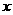 的方程
的方程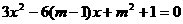 的两根的模的和为
的两根的模的和为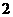 ,求实数
,求实数 的值.
的值.
16.有如下命题,
(1)已知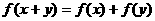 ,且
,且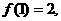 则
则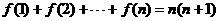
(2)已知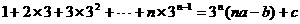 对一切自然数n都成立,那么这样的实数a,b,c不存在; (3)否定结论“至多有两个解”,可以用“至少有两个解”;
对一切自然数n都成立,那么这样的实数a,b,c不存在; (3)否定结论“至多有两个解”,可以用“至少有两个解”;
(4)复数z是一个实数的充要条件是z=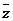 ,且z是一个虚数的充要条件是z+
,且z是一个虚数的充要条件是z+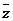 是一个实数;
是一个实数;
(5)若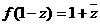 ,则
,则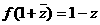 ;其中正确的命题有
;其中正确的命题有
15.如图,它满足(1)第n行首尾两数均为n,(2)表中的递推关系类似杨辉三角,则第n行(n 2)第二个数是 _____
2)第二个数是 _____
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
6 16 25 25 16 6
14.在平面内,三角形的面积为s,周长为c,则它的内切圆的半径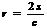 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=
.
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=
.
13. .
.
12.在抛物线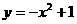
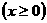 上找一点P
上找一点P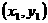 ,其中
,其中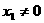 ,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
A.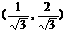 B.
B.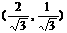 C.
C.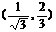 D.
D.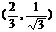
11.如果函数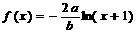 的图象在
的图象在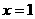 处的切线
处的切线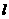 过点(
过点(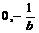 ),并且l与圆C:
),并且l与圆C: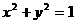 相离,则点
相离,则点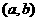 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
A.在圆内 B.在圆外 C.在圆上 D.不能确定
10.在平面几何里,有射影定理:“设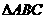 的两边AB、AC相互垂直,AD是斜边BC上的高,则
的两边AB、AC相互垂直,AD是斜边BC上的高,则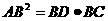 ”。拓展到空间,类比平面几何的射影定理,“在三棱锥
”。拓展到空间,类比平面几何的射影定理,“在三棱锥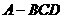 中,
中,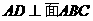 ,A在
,A在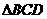 内的射影为O”,则可得 ( )
内的射影为O”,则可得 ( )
A.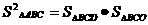 B.
B.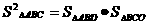
C.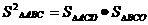 D.
D.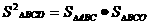
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com