5.对“a,b是异面直线”的叙述，正确的是(　　 )

①a∩b=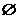且a不平行于b　 ②a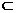平面α,b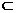平面β且α∩β=　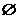 ③a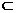平面α,b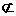平面α　 ④不存在平面α,使a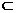平面α且b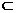平面α成立

A.①②　　　　　　　 B.①③　　　　　　 C.①④　　　　　　 D.③④

答案:C

解析:根据“异面直线是不同在任何一个平面内的两条直线”的定义知,结论④正确.空间不相交的两条直线除平行外就是异面,故对于结论①,既然两直线不平行,则必然异面.分别在两个平面内的两条直线可能平行,故②不正确.平面内的一条直线和平面外的一条直线除异面外还可能平行或相交,故③不正确.综上所述,只有①④正确.

4.如图,点P,Q,R,S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的图是(　　 )

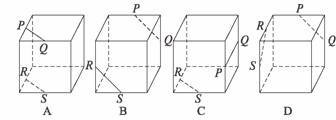
答案:C

解析:A,B中的PQ与RS相互平行;D中的PQ与RS相交;由两条直线异面的判定定理可知C中的PQ与RS异面.

3.如右图,α∩β=l,A∈β,B∈β,AB∩l=D,C∈α,则平面ABC和平面α的交线是(　　 )

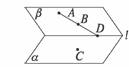
A.直线AC　　　　　　　　　　　　　 B.直线BC

C.直线AB　　　　　　　　　　　　　 D.直线CD

答案:D

解析: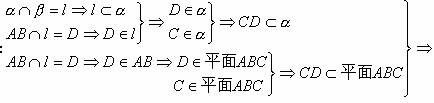

CD为平面ABC与平面α的交线.故选D.

A.空间不同三点确定一个平面

B.空间两两相交的三条直线确定一个平面

C.四边形确定一个平面

D.和同一直线都相交的三条平行线在同一平面内

答案:D

解析:根据公理3(经过不在同一条直线上的三点,有且只有一个平面)知不在同一直线上的三点,才能确定一个平面,所以A错.

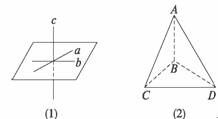
如图(1),a,b,c三条直线两两相交,但a,b,c不共面,所以B错误.

如图(2),显然四边形ABCD不能确定一个平面.

2.已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于(　　 )

A.30°　　　　　　　　　　　　　　 B.30°或150°

C.150°　　　　　　　　　　　　　　 D.以上结论都不对

答案:B

解析:由等角定理可知∠PQR与∠ABC相等或互补,即∠PQR=30°或150°.

20．已知抛物线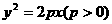．过动点M(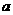，0)且斜率为1的直线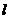与该抛物线交于不同的两点A、B，．

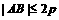(Ⅰ)求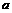的取值范围；

(Ⅱ)若线段AB的垂直平分线交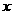轴于点N，求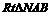面积的最大值．(14分)

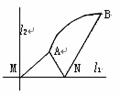
19．如图，直线l₁和l₂相交于点M，l₁⊥l₂，点N∈l₁．以A、B为端点的曲线段C上的任一点到l₂的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=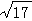，|AN|=3，且|BN|=6．建立适当的坐标系，求曲线段C的方程．(14分)

18．河上有抛物线型拱桥，当水面距拱桥顶5米时，水面宽为8米，一小船宽4米，高2米，载货后船露出水面上的部分高0.75米，问水面上涨到与抛物线拱顶相距多少米时，小船开始不能通航？(12分)

17．动直线y =a，与抛物线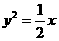相交于A点，动点B的坐标是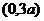，求线段AB中点M的轨迹的方程．(12分)

16．已知抛物线的顶点在原点，对称轴是x轴，抛物线上的点M(－3，m)到焦点的距离等于5，求抛物线的方程和m的值．(12分)

15．已知动圆M与直线y =2相切，且与定圆C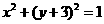：外切，求动圆圆心M的轨迹方程．(12分)