
题目列表(包括答案和解析)
4、不等式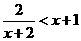 的解集是( )
的解集是( )
A、 B、
B、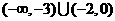
C、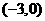 D、
D、
3、下列函数中,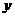 的最小值为
的最小值为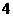 的是( )
的是( )
A、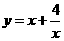 B、
B、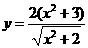
C、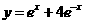 D、
D、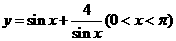
2、若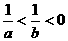 ,则下列不等式①
,则下列不等式①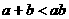 ;②
;②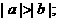 ③
③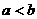 ;④
;④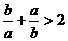 中,正确的不等式有( )
中,正确的不等式有( )
A、1个 B、2个 C、3个 D、4个
1、已知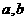 为非零实数,且
为非零实数,且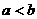 ,则下列命题成立的是( )
,则下列命题成立的是( )
A、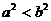 B、
B、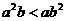 C、
C、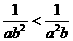 D、
D、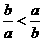
22.(本小题满分14分)如图,在Rt△AOB中,∠OAB=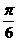 ,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-A0-C是直二面角,动点D在斜边AB上,
,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-A0-C是直二面角,动点D在斜边AB上,
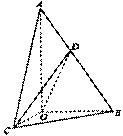 (1)求证:平面COD⊥平面AOB;
(1)求证:平面COD⊥平面AOB;
(2)当D为AB的中点时,求异面直线AO与CD所成角的大小;
(3)求CD与平面AOB所成角的最大值。
21.(本题满分12分)已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球。现从甲、乙两个盒内各任取2个球。(1)求取出的4个球均为黑球的概率;(2)求取出的4个球中恰有1个红球的概率。
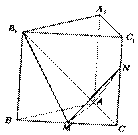
20.如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点,且CN=2C1N,(1)求二面角B1-AM-N的平面角的余弦值;(2)求点B1到平面AMN的距离。
19.(本小题满分12分)若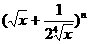 展开式中前三项的系数成等差数列,
展开式中前三项的系数成等差数列,
求:(1)展开式中含x的一次幂的项;
(2)展开式中所有x的有理项。
18.(本小题满分12分)甲、乙两人各进行3次射击,甲每次击中目标的概率为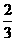 ,乙每次击中目标的概率为
,乙每次击中目标的概率为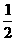 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。
(1)求乙至多击中目标2次的概率;
(2)求甲恰好比乙多击中目标1次的概率。
17.(本小题满分12分)如图,棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是DD1、DB的中点,求证:
(1)EF∥平面ABC1D1;
(2)EF⊥B1C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com