
题目列表(包括答案和解析)
6. 学校组织演讲比赛,现要从高二选出6人参加比赛,已知高二年级共有4各班,每班至少有一人参赛,则高二年级的演讲选手产生的不同的方法为 ( )
A.8 B. 6 C. 10 D.20
5.在平面直角坐标系中,从六个点:A(0,0)、B(0,2)、C(1,1)、D(2,0)、E(2,2)、F(3,3)中任取三个,这三点能构成三角形的概率为 ( )
A.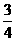 B.
B.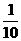 C.
C.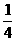 D.
D.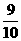
4. 在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手,若从中任选3人,则选出的火炬手的编号组成以3为公差的等差数列的概率为 ( )
A.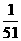 B.
B.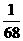 C.
C.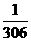 D.
D.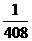
3. 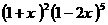 的展开式中
的展开式中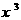 的系数为 ( )
的系数为 ( )
A.170 B.80 C.-10 D.10
2. 一个口袋中装有15个大小相同且质量密度也相同的球,其中10个白球,5个黑球,从中摸出2个球,则1个是白球,1个是黑球的概率是 ( )
A.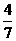 B.
B.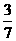 C.
C.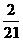 D.
D.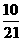
1. 一个节目单原有5个节目,现增加2个节目,在不打乱原有节目先后顺序的情况下,不同的演出顺序有 ( )
A.42种 B. 30种 C.6种 D.5040种
24. 解:(1)当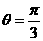 时,假设
时,假设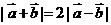 成立,则
成立,则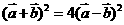 展开得:
展开得: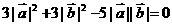 …(*)以下有三种方法分析:①变为
…(*)以下有三种方法分析:①变为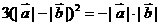 显然不成立的;②令
显然不成立的;②令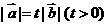 方程(*)变为
方程(*)变为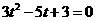 ,次方程无解.③假设
,次方程无解.③假设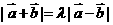 (
(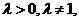 否则
否则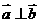 与条件不符合)则有,
与条件不符合)则有,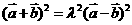 展开整理得:
展开整理得: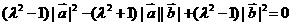 ,将
,将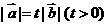 代入得
代入得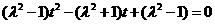 关于
关于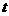 有正根
有正根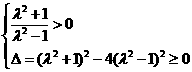 解得
解得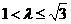 ,而
,而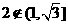 ,综上所得,假设不成立,所以命题是假命题.
,综上所得,假设不成立,所以命题是假命题.
(2)假设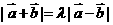 (
(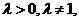 否则
否则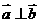 与条件不符合)两边平方并将
与条件不符合)两边平方并将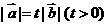 代入整理得:
代入整理得: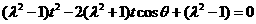 ,方程有两个正根
,方程有两个正根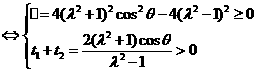
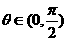 得到
得到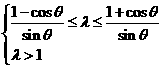
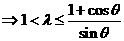 ,综上得当
,综上得当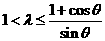 时命题为真命题.
时命题为真命题.
本资料由《七彩教育网》 提供!
16、(本小题15分)等差数列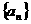 中,前三项分别为
中,前三项分别为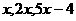 ,前
,前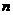 项和为
项和为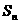 ,且
,且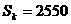 。
。
(1)、求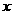 和
和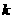 的值; (2)、求T=
的值; (2)、求T=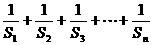

15.(本题满分15分)在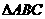 中,
中,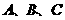 是三角形的三内角,
是三角形的三内角,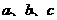 是三内角对应的三边,已知
是三内角对应的三边,已知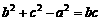 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若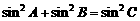 ,求角
,求角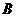 的大小.
的大小.
班级 姓名 学号 成绩
13、 14、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com