
5.若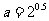 ,
,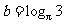 ,
,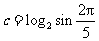 ,则
,则
A.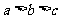 B.
B.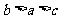 C.
C.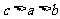 D.
D.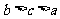
4.已知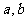 为非零实数,且
为非零实数,且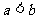 ,则下列命题成立的是 ( )
,则下列命题成立的是 ( )
A.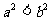 B.
B.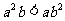 C.
C.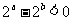 D.
D.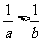
3.已知命题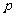 :
: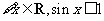 ,则 ( )
,则 ( )
A.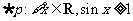 B.
B. 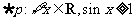
C.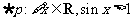 D.
D. 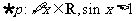
2.集合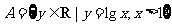 ,
,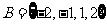 则下列结论正确的是 (
)
则下列结论正确的是 (
)
A.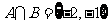 B.
B.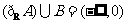
C.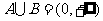 D.
D.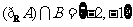
1.命题“若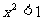 ,则
,则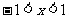 ”的逆否命题是 ( )
”的逆否命题是 ( )
A.若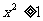 ,则
,则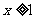 或
或 B.若
B.若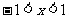 ,则
,则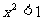
C.若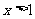 或
或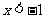 ,则
,则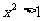 D.若
D.若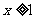 或
或 ,则
,则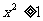
22.(本题满分14分)
已知函数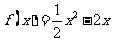 ,
,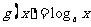 (a>0且a
(a>0且a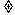 1),其中
1),其中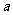 为常数.如果
为常数.如果
h(x)=f(x)+g(x)是增函数,且h(x)的导函数h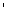 (x)存在零点.
(x)存在零点.
(1)求a的值;
(2)设A(x1、y1)、B(x2、y2)(x1 <
x2)是函数y=g(x)的图象上两点,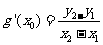
(g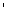 (x)为g(x)的导函数),证明:x1 < x0 <
x2
(x)为g(x)的导函数),证明:x1 < x0 <
x2
21.(本题满分12分)
对定义域是Df ,Dg的函数y=f(x),y=g(x),规定:
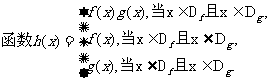
(Ⅰ)若函数f(x)= 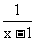 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(Ⅱ)求问题(1)中函数h(x)的值域;
(Ⅲ)若g(x)=f(x+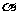 ),其中
),其中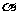 是常数,且
是常数,且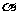
 [0,
[0,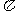 ],请设计一个定义域为R的函数,y=f(x),及一个
],请设计一个定义域为R的函数,y=f(x),及一个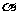 的值,使得h(x)=cos4x,并予以证明.
的值,使得h(x)=cos4x,并予以证明.
20.(本题满分11分)
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注。已知2006年1月Q型车的销量为a辆,通过分析预测,若以2006年1月为第1月,其后两年内Q型车每月的销量都将以1%的比率增长,而R型车前n个月的销售总量Tn大致满足关系式:Tn =228a(1. 012n -1).
(1)求Q型车前n个月的销售总量Sn的表达式;
(2)比较两款车前n个月的销售总量Sn与Tn的大小关系;
(3)试问从第几个月开始Q型车的月销售量小于R型车月销售量的20%,并说明理由.(参考数据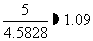
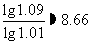 )
)
19.(本题满分12分)
设 ABC的内角A、B、C所对的边长分别为a、b、c ,且acosB – bcosA =
ABC的内角A、B、C所对的边长分别为a、b、c ,且acosB – bcosA =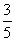
(1)试求tanA与tanB的关系;
(2)求tan(A-B)的最大值.
18.(本小题满分12分) .
数列{an}的前n项和记为Sn,a1 = l,an+1 = 2Sn+1(n≥1)
(I)求{ an }的通项公式;
(Ⅱ)等差数列{bn}的各项为正,其前n项和为Tn,切T3=15,又a1+b1,a2+b2,a3+b3,成等比数列,求Tn
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com