
1、设集合M=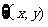 | x+y>2,且xy>0
| x+y>2,且xy>0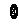 ,N=
,N=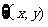 | x>1,且y>1
| x>1,且y>1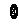 ,则有
,则有
A.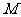
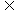
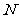 B.
B.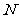
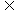
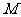 C.
C.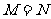 D.
D.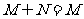
22.(14分)已知函数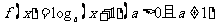 ,点P是
,点P是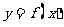 图象上的任意
图象上的任意
一点,P关于原点的对称点Q的轨迹是函数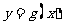 的图象
的图象
(1)求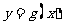 的解析式
的解析式
(2)当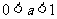 时,解不等式2
时,解不等式2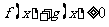
(3)当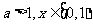 时,
时,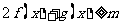 恒成立,求
恒成立,求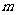 的范围.
的范围.
21.(12分)已知两点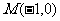 ,
,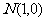 且点
且点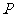 使
使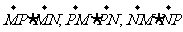 成公差小于零的等差数列。
成公差小于零的等差数列。
(1)点P的轨迹是什么曲线?
(2)若点P的坐标为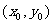 ,记
,记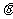 为
为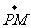 与
与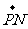 的夹角,求
的夹角,求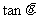 。
。
20.(12分)已知二次函数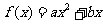 (a,b为常数且a≠0)满足条件
(a,b为常数且a≠0)满足条件
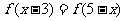 ,且方程
,且方程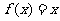 有等根
有等根
(1)求的解析式
(2)是否存在实数m,n(m<n)使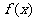 的定义域和值域分别为[m,n]和[3m,3n],如果存在,求出m,n的值;如果不存在,说明理由.
的定义域和值域分别为[m,n]和[3m,3n],如果存在,求出m,n的值;如果不存在,说明理由.
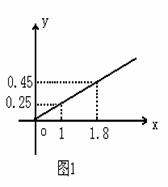
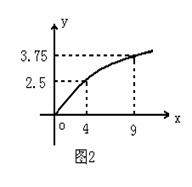
19.(12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这
10万元投资,才能是企业获得最大利润,其最大利润约为多少万元。(精确到1万
元)。
18.(12分)如图,在直二面角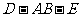 中,四边形
中,四边形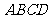 是边长为2的正方形,
是边长为2的正方形,
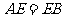 ,
,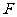 为
为 上的点,且
上的点,且
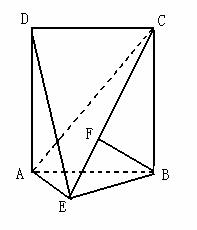
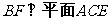
(1)求证: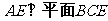 ;
;
(2)求二面角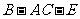 的大小;
的大小;
(3)求点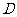 到平面
到平面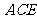 的距离。
的距离。
17.(12分)设a>0,f(x)=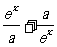 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明f(x)在(0,+∞)上是增函数.
16.已知偶函数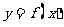
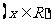 在区间
在区间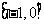 上单调递减,且满足
上单调递减,且满足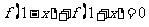 ,给出下列判断①
,给出下列判断①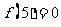 ;②
;②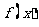 在
在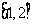 上是减函数;③
上是减函数;③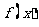 的图象关于直线
的图象关于直线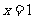 对称;④函数
对称;④函数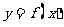 在
在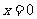 处取得最小值。其中正确论断的序号是
(写出所有正确论断的序号)
处取得最小值。其中正确论断的序号是
(写出所有正确论断的序号)
15.已知点P,直线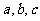 以及平面
以及平面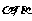 ,给出下列命题:①若
,给出下列命题:①若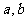 与
与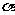 成等角,则
成等角,则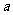 ∥
∥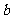 ;②若
;②若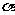 ∥
∥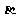 ,
,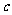 ⊥
⊥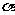 ,则c⊥
,则c⊥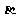 ③若
③若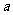 ⊥
⊥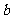 ,
,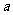 ⊥
⊥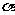 ,则
,则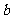 ∥
∥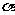 ④若
④若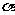 ⊥
⊥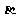 ,
,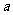 ∥
∥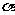 ,则
,则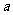 ⊥
⊥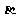 ⑤若
⑤若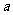 ⊥
⊥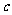 ,
,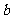 ⊥
⊥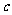 ,则
,则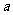 ∥
∥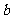 或
或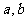 异面直线。
异面直线。
其中错误命题的序号是 。
14.在R上定义运算 :
: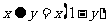 ,若不等式
,若不等式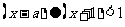 对任意实数x都成立,则实数a的取值范围___________。
对任意实数x都成立,则实数a的取值范围___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com