
2.若p、q为简单命题,则“p且q为假”是“p或q为假”的
A.充分不必要的条件 B.必要不充分的条件
C.充要条件 D.既不充分也不必要的条件
1.tan(-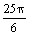 )的值是
)的值是
A.-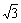 B.-
B.-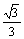 C.
C.
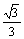 D.
D.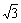
22.(本小题满分14分)
设数列{an}的各项都是正数,且对任意n∈N*都有a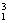 +a
+a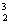 +a
+a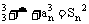 ,其中Sn为数列{an}的前n项和.
,其中Sn为数列{an}的前n项和.
(Ⅰ)求证:a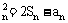 ;
;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=3n+(-1)n-1λ·2an(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.
21.(本小题满分12分)
在直角坐标平面内,△ABC的两个顶点A,B的坐标分别为A(-1,0),B(1,0)平面内两点G,M同时满足以下条件:
①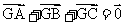 ;②
;②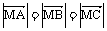 ;③
;③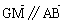
(Ⅰ)求△ABC的顶点C的轨迹方程;
(Ⅱ)过点P(2,0)的直线l与△ABC的顶点C的轨迹交于E,F两点,求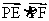 的取值范围.
的取值范围.
20.(本小题满分12分)
已知a<2,f(x)=(x2+ax+a)e-x
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由.
19.(本小题满分12分)
如图所示,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,点D在AB上且DE=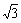 .
.
(Ⅰ)求证:CD⊥面A1ABB1;
(Ⅱ)求二面角C-AE-D的大小;
(Ⅲ)求点A1到平面CDE的距离.
18.(本小题满分12分)
甲袋中装有2个白球1个黑球,乙袋中装有3个白球1个红球,现从甲袋中连续三次有放回地摸出一球,从乙袋中连续两次有放回地摸出一球.
(Ⅰ)求从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率;
(Ⅱ)求从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率;
(Ⅲ)设从甲袋中摸出白球的次数为随机变量ζ,求Eζ.
17.(本小题满分12分)
已知向量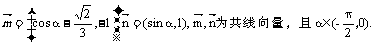
(Ⅰ)求sinα-cosα的值;
(Ⅱ)求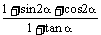 的值.
的值.
16.将一个四棱锥V-ABCD的每个顶点染上一种颜色,并使每一条棱的两端异色,若只有4种颜色可供使用,则不同的染色方法种数为__________.(用数字作答)
15.如果直线l将圆x2+y2-2x-4y=0平分,且不经过第四象限,那么l的斜率的取值范围是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com