
6.已知函数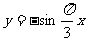 在区间[0,t]上至少取得2个最大值,则正整数t的最小值( )
在区间[0,t]上至少取得2个最大值,则正整数t的最小值( )
A.8 B.9 C.10 D.11
5.等差数列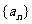 中,
中,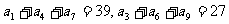 ,则数列
,则数列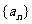 前9项的和
前9项的和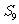 等
等
于 ( )
A.66 B.99 C.144 D.297
4.如果不等式组 有解,则实数a的取值范围是 ( )
有解,则实数a的取值范围是 ( )
A.(-∞,-1)∪(3,+∞) B.(-∞,-3)∪(1,+∞)
C.(-1,3) D.(-3,1)
2.已知向量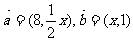 ,其中
,其中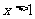 ,若
,若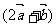 ∥
∥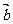 ,则
,则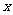 的值为 ( )
的值为 ( )
A.0 B.2 C.4 D.8
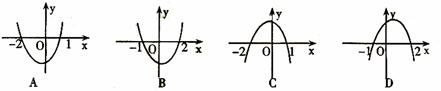 3.已知函数
3.已知函数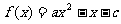 ,且
,且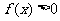 的解集为(-2,1)则函数
的解集为(-2,1)则函数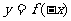 ( )
( )
1.设集合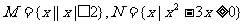 ,则M∩N ( )
,则M∩N ( )
A. B.[-2,0] C.[0,2] D.
B.[-2,0] C.[0,2] D.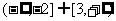
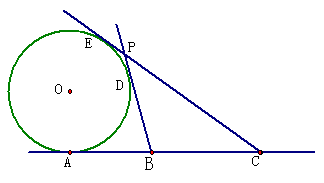
21、已知A、B、C是直线m上的三点,且|AB|=|BC|=6,⊙O切直线m于A,又过B、C作圆O异于m的两切线,切点分别为D、E,设两切线交于点P
(1)、建立适当的坐标系,求P点的轨迹分程
(2)、经过点C的直线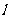 与点P的轨迹交于M、N两点,且满足
与点P的轨迹交于M、N两点,且满足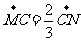 ,求直线
,求直线 的方程。
的方程。
20、某种细菌每隔两小时分裂一次(每一个细菌分裂成两个),分裂瞬间的时间忽略不计,研究开始计时时有两个细菌,在研究过程中不断进行分裂。细菌总数y是研究进行时间t的函数,记y=f(t),
(1)、写出函数y=f(t)的定义域和值域,
(2)、在给出的坐标系中画出y=f(t)(0≤t≤6)
(3)、写出研究进到第n小时(n≥0,n∈Z)时细菌的总数有多少个(用关于n的式子表示)
19、已知函数 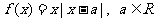
(Ⅰ)解关于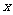 的不等式
的不等式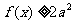 (Ⅱ)当
(Ⅱ)当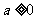 时,求
时,求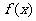 的单调区间。
的单调区间。
18、若公比为C的等比数列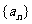 的首项
的首项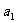 =1,且满足
=1,且满足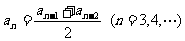
①求C的值 。
②求数列 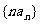 的前n项和。
的前n项和。
17、已知 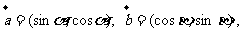
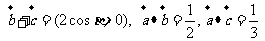 求
求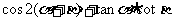 之值。
之值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com