2．为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5-18岁的男生体重(㎏)，得到频率分布直方图如下：

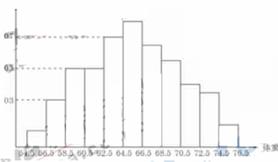
根据上图可得这100名学生中体重在(56.5，64.5)的学生人数是　　　　　 (　 　)

　 A．20　　　　　　　 B．30　　　　　　 C．40　　　　　　　 D．50

1．已知集合A=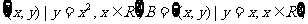则A∩B的元素个数为(　 )

　 A．0个　　　　　　 B．1个　　　　　 C．2个　　　　　　 D．无穷多个

21．(本小题满分14分)

定义在(－1，1)上的函数f (x)满足：对任意x，y∈(－1，1)都有

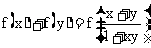
(1) 求证：函数f (x)是奇函数；

(2) 若当x∈(－1，0)时，有f (x)>0，求证：f (x)在(－1，1)上是减函数；

(3) 在(2)的条件下解不等式：．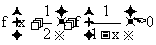

20．(本小题满分14分)

已知函数y= f (x)对于任意实数x，y都有f (x+y) =f (x)+f (y)+2xy .

(1) 求f (0)的值；　

(2) 若f (1)=1，求f (2)，f (3)，f (4)的值，猜想f(n)的表达式并用数学归纳法证明你的结论(n∈N*)；

(3) 若f (1)≥1，求证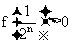： (n∈N*)．　　

19．(本小题满分14分)

某公司生产的A型商品通过租赁柜台进入某商场销售．第一年，商场为吸引厂家，决定免收该年管理费，因此，该年A型商品定价为每件70元，年销售量为11.8万件．第二年，商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元)，于是该商品的定价上升为每件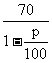元，预计年销售量将减少p万件.

(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数，并指出这个函数的定义域；

(2) 要使第二年商场在此项经营中收取的管理费不少于14万元，则商场对该商品征收管理费的比率p%的范围是多少?

(3) 第二年，商场在所收管理费不少于14万元的前提下，要让厂家获得最大销售金额，则p应为多少?　

18．(本小题满分14分)

已知函数f (x) = (x－a)(x－b)(x－c).

(1) 求证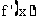：= (x－a)(x－b)+(x－a)(x－c)+(x－b)(x-c)；

(2) 若f (x)是R上的增函数，是否存在点P，使f (x)的图象关于点P中心对称?

如果存在，请求出点P坐标，并给出证明，如果不存在，请说明理由．

17．(本小题满分12分)

小张有一只放有a个红球，b个黄球，c个白球的箱子，且a+b+c =6 (a，b，c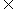N)，小刘有一只放有3个红球，2个黄球，1个白球的箱子，两人各自从自己的箱子中任取一球，规定：当两球同色时小张胜，异色时小刘胜.

(1) 用a、b、c表示小张胜的概率；

(2) 若又规定当小张取红、黄、白球而胜的得分分别为1分、2分、3分，否则得0分，求小张得分的期望的最大值及此时a、b、c的值.

16．(本小题满分12分)

二次函数f (x)满足f (x+1)－f (x)=2x，且f (0) =1.

(1) 求f (x)的解析式；

(2) 在区间[－1，1]上，y=f (x)的图象恒在y=2x十m的图象上方，试确定实数m的取值范围．

15．购买手机的“全球通”卡，使用时须付“基本月租费”(每月须交的固定月租费)50元，在市区通话时每分钟另收话费0.4元；购买“神州行”卡，使用时不收“基本月租费”，但市区内通话时每分钟另收话费0.6元．若某用户每月手机费预算为120元，则在这两种手机卡中，购买__________卡较合算.

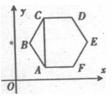
14．如图正六边形ABCDEF中，AC∥y轴．从六个顶点中任取三点，使这三点能确定一条形如y=ax ²+bx+c (a≠0)的抛物线的概率是_______________.