22．(本小题满分14分)

　　 对于数列{a_n}，定义{△a_n }为数列{a_n}的一阶差分数列，其中

　 (Ⅰ)若数列{a_n}的通项公式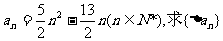的通项公式；

　 (Ⅱ)若数列{a_n}的首项是1，且满足，

　　　　 (1)证明数列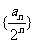为等差为数列；

　　　　 (2)求{a_n}的前n项和S_n

21．(本小题满分12分)学校食堂定期从某粮店以每吨1500元的价格买大米，每次购进大米需支付运输劳务费100元，已知食堂每天需要大米1吨，贮存大米的费用为每吨每天2元，假定食堂每次均在用完大米的当天购买。

　 (Ⅰ)该食党每多少天购买一次大米，能使平均每天所支付的费用最少？

　 (Ⅱ)粮店提出价格优惠条件：一次购买量不少于20吨时，大米价格可享受九五折优惠(即是原价的95%)，问食堂可否接受此优惠条件？请说明理由。

20．(本小题满分12分)

已知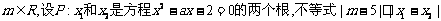

　　 对任意实数a∈[1，2]恒成立；Q：函数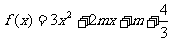有两个不同的零点.

　　 求使“P且Q”为真命题的实数m的取值范围.

19．(本小题满分12分)已知定义在R上奇函数，当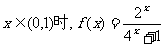

　 (Ⅰ)求f(x)在(－1，1)上的解析式

　 (Ⅱ)证明f(x)在(0，1)上是减函数

18．(本小题满分12分)

　　 设函数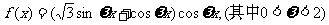

　 (I)若f(x)的周期为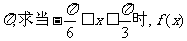的值域

　 (Ⅱ)若函数f(x)的图象的一条对称轴方程为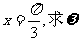的值

17．(本小题满分12分)

　　　　 在△ABC中，角A、B、C所对边分别为a，b，c，已知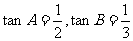，且最长边边长为l.

　　 求：(I)角C的大小；

　　　 (Ⅱ)△ABC最短边的长.

16．已知a，b，c是△ABC的三边，S是△ABC的面积，若a=4，b=5，S=5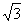，则边c的值为　　　　 　；

15．在数列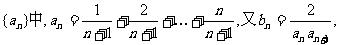则数列{b_n}的前n项和为

　　 　　　　　　　；

14．等差数列有如下性质：若{a_n}是等差数列，则数列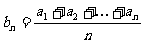是等差数列，类比上述性质，相应地，若数列{c_n}是正项等比数列，则数列d_n=　　 　也是等比数列.

13．函数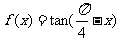的单调减区间为　　　　　　 　；