
5.若数列{an}满足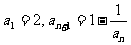 ,则a2007的值 ( )
,则a2007的值 ( )
A.1 B.-1 C.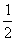 D.2
D.2
4.若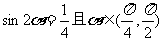 ,则
,则 的值是 ( )
的值是 ( )
A.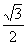 B.
B.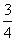 C.-
C.-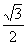 D.-
D.-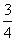
3.若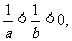 则下列不等式:①
则下列不等式:①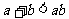 ②
②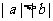 ③
③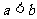 ④
④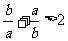 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.①② B.②③ C.①④ D.③④
2.已知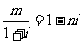 ,其中m,n是实数,是m+ni等于 ( )
,其中m,n是实数,是m+ni等于 ( )
A.1+2i B.1-2i C.2+i D.2-i
1.设P、Q为两个非空实数集合,定义集合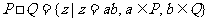 ,若P={-1,0,1},Q={-2,2},则集合
,若P={-1,0,1},Q={-2,2},则集合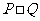 中元素的个数是 ( )
中元素的个数是 ( )
A.3 B.4 C.5 D.6
22.(本小题满分14分)
对于数列{an},定义 为数列{an}的一阶差分数列,其中
为数列{an}的一阶差分数列,其中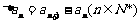 .
.
(Ⅰ)若数列{an}的通项公式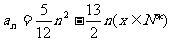 ,求
,求 的通项公式;
的通项公式;
(Ⅱ)若数列{an}的首项是1,且满足 ,(1)证明数列
,(1)证明数列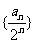 为等差数列;(2)求{an}的前n项和Sn。
为等差数列;(2)求{an}的前n项和Sn。
21.(本小题满分12分)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
 产品
产品资源 |
甲产品 (每吨) |
乙产品 (每吨) |
资源限额 (每天) |
|
煤(t) |
9 |
4 |
360 |
|
电力(kw·h) |
4 |
5 |
200 |
|
劳力(个) |
3 |
10 |
300 |
|
利润(万元) |
7 |
12 |
|
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
20.(本小题满分12分)
已知P:对任意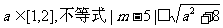 恒成立;
恒成立;
Q:函数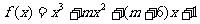 存在极大值和极小值。
存在极大值和极小值。
求使“P且 Q”为真命题的m的取值范围。
Q”为真命题的m的取值范围。
19.(本小题满分12分)
设数列{an}、{bn}满足: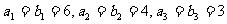 ,且数列
,且数列
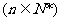 是等差数列,{bn-2}是等比数列。
是等差数列,{bn-2}是等比数列。
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)是否存在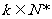 ,使
,使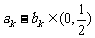 ,若存在,求出k;Y若不存在,说明理由。
,若存在,求出k;Y若不存在,说明理由。
18.(本小题满分12分)
已知向量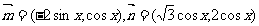 ,定义函数
,定义函数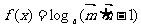
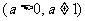 。
。
(Ⅰ)求函数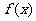 的最小正周期;
的最小正周期;
(Ⅱ)求函数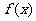 的最大值或最小值及此时对应的x的值;
的最大值或最小值及此时对应的x的值;
(Ⅲ)确定函数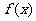 的单调递增区间。
的单调递增区间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com