
7.设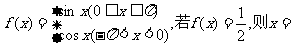
6.函数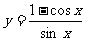 的最小正周期为
的最小正周期为
5.在同一坐标系内,函数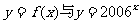 的图象关于直线
的图象关于直线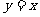 对称,则
对称,则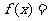
。
4.已知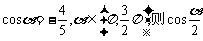 =
=
3.函数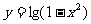 的定义域是
的定义域是
2.已知集合 =
=
1.已知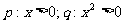 ,那么p是q的
条件。
,那么p是q的
条件。
(从“充分非必要”、“必要非充分”、“充要或既不充分也不必要”中选取)
22.(本题满分18分)
在杨辉三角形中,除“两腰”上的数字外,其余任意数都等于它上一行“左右两肩”上的数之和。将杨辉三角形中的每一个数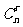 都换成分数
都换成分数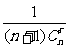 ,得到莱布尼茨三角形
,得到莱布尼茨三角形
杨辉三角形 莱布尼茨三角形



(1) 类比杨辉三角形的上述性质,得真命题:莱布尼茨三角形中,每一个数都等于______________(只须填上类比而得的结论,不必证明)
(2)
在莱布尼茨三角形中,称“左腰”上的数字为“第1层”,紧靠“第1层”且与之平行的称为“第2层”,猜测“第2层”中各数按从上到下的顺序构成的数列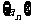 的一个通项公式(不必证明),并据此求该数列的前
的一个通项公式(不必证明),并据此求该数列的前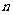 项和
项和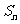 。
。
设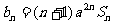
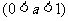 ,若存在唯一的自然数
,若存在唯一的自然数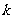
 ,使得
,使得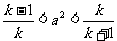 成立,问数列
成立,问数列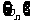 中是否存在唯一的最大项,试证明你的结论。
中是否存在唯一的最大项,试证明你的结论。
21.(本题满分16分)
已知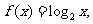 当点
当点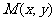 在
在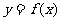 的图象上运动时,点
的图象上运动时,点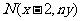 在函数
在函数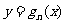 的图象上运动(
的图象上运动(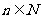 ).
).
1)
求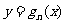 的表达式;
的表达式;
2)
求集合A={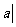 关于
关于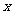 的方程
的方程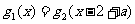 有实根,
有实根,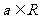 };
};
3)
设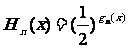 ,函数
,函数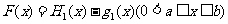 的值域为
的值域为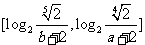 ,求实数
,求实数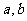 的值。
的值。
20.(本题满分14分)
某企业2005年的纯利润为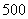 万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润少
万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润少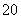 万元,今年初该企业一次性投入资金
万元,今年初该企业一次性投入资金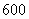 万元进行技术改造,预测在未扣除技术改造资金的情况下,第
万元进行技术改造,预测在未扣除技术改造资金的情况下,第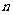 年(今年为第一年)的利润为
年(今年为第一年)的利润为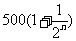 万元(
万元(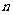 为正整数)。
为正整数)。
(Ⅰ)设从今年起的前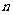 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为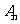 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为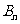 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求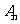 、
、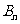 的表达式;
的表达式;
(Ⅱ)依上述预测一下:从长远效益来看,该企业有没有进行技术改造的必要?如有必要,则至少要经过多少年后,才能初见进行技术改造的成效?请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com