
6.已知f(x)=(x-a)(x-b)-2,并且m,n是方程f(x)=0的两根,实数a,b,m,n的大小可能是
A.n<a<b<m B.a<n<m<b C.a<n<b<m D.n<a<m<b
5.已知定义域为R的偶函数y=f(x)的一个单调递增区间是(2,6),则函数y=f(2-x)图象
A.对称轴为x= -2,且一个单调减区间是(4,8) B.对称轴为x= -2,且一个单调减区间是(0,4)
C.对称轴为x= 2,且一个单调增区间是(4,8) D.对称轴为x= 2,且一个单调增区间是(0,4)
4.函数y=|2 x-2|
A.在(-∞,+∞)上单调递增
B.在(-∞,1]上是减函数,在[1,+∞)上是增函数
C.在(-∞,1]上是增函数,在[1,+∞)上是减函数
D.在(-∞,0]上是减函数,在[0,+∞)上是减函数
3.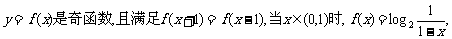
则y=f(x)在(1,2)内是
A.单调增函数,且f(x)<0 B.单调减函数,且f(x)>0
C.单调增函数,且f(x)>0 D.单调减函数,且f(x)<0
2.对某地农村家庭拥有电器情况抽样调查如下:有电视机的占60%;有洗衣机的占有55%;有电冰箱的占45%;至少有上述三种电器中的两种以上的占55%;三种都有的占20%.那么没有任何一种电器的家庭占的比例是
A.5% B.10% C.12% D.15%
1.若一系列函数的解析式相同,值域也相同,但定义域不同,则称这些函数为“同族函数”,那么解析式为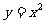 ,值域为{1,4}的“同族函数”共有
,值域为{1,4}的“同族函数”共有
A.4个 B.8个 C.9个 D.16个
22、设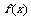 是定义在
是定义在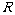 上的奇函数,且函数
上的奇函数,且函数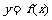 与
与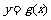 的图象关于直线
的图象关于直线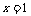 对称,当
对称,当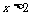 时,
时,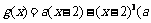 为常数)
为常数)
(1)求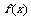 的解析式;
的解析式;
(2)若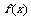 对区间
对区间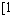 ,
, 上的每个
上的每个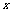 值,恒有
值,恒有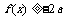 成立,求
成立,求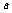 的取值范围。
的取值范围。
21、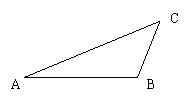 飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东300,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s.
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角;
(3)若信号从P点的正上方Q点处发出,则A、B
收到信号的时间差变大还是变小,并证明你的结论.
20、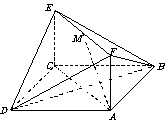 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=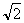 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证AM//平面BDE; (2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是 60°.
19、甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数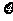 的数学期望和方差.
的数学期望和方差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com