
8.函数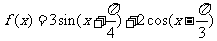 的最小正周期是_____
的最小正周期是_____
7.已知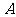 、
、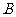 为
为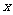 轴上不同的两点,点
轴上不同的两点,点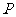 的横坐标为
的横坐标为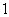 ,且
,且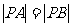 ,若直线
,若直线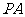 的方程为
的方程为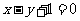 ,则直线
,则直线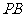 的方程为 _______
的方程为 _______
6.设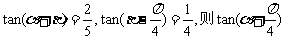 =____________
=____________
5.已知复数z1=6+2i,z2=t+i,且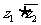 是实数,则实数t=_________
是实数,则实数t=_________
4.将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有_____种
3.若方程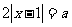 有且仅有二解,则实数
有且仅有二解,则实数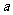 的取值范围是________
的取值范围是________
2.设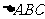 的三个内角
的三个内角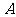 、
、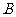 、
、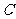 所对边的长分别是
所对边的长分别是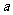 、
、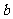 、
、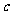 ,且
,且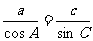 ,那么
,那么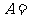 ______
______
1.若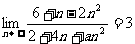 ,则
,则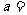 _____
_____
22.(本题满分18分)本题共有3个小题,第1小题满分6分,
第2小题满分6分,第三小题满分6分.
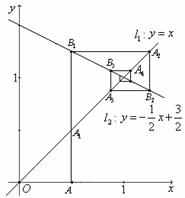 如图所示,直线
如图所示,直线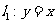 ,
,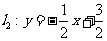 ,点
,点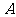 是
是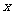 轴上的一点,过
轴上的一点,过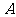 作
作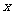 轴的垂线交
轴的垂线交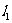 、
、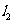 分别于
分别于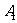 、
、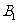 ,过
,过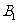 作
作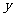 轴的垂线交
轴的垂线交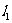 于
于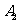 ,过
,过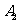 作
作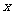 轴的垂线交
轴的垂线交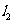 于
于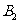 ……,依此类推分别作
……,依此类推分别作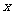 轴及
轴及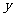 轴的垂线,这样在直线
轴的垂线,这样在直线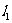 、
、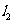 上分别得到点列
上分别得到点列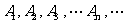 及
及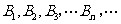 .设点
.设点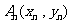 .
.
(1) 已知点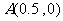 ,试写出数列
,试写出数列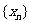 的递推关系式;
的递推关系式;
(2) 求数列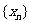 的通项公式,并计算
的通项公式,并计算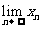 ;
;
(3) 考察(2)中的极限与两直线交点坐标之间的关系,试构造一个递推关系式并用计算器迭代求出方程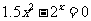 在区间
在区间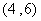 上的近似解(精确到0.01).
上的近似解(精确到0.01).
[解](1)
(2)
(3)
21.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分3分,第3小题8分.
已知某类学习任务的掌握程度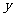 与学习时间
与学习时间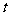 (单位时间)之间有如下函数关系:
(单位时间)之间有如下函数关系:
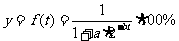
这里我们称这一函数关系为“学习曲线”.已知这类学习任务中的某项任务有如下两组数据: 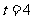 ,
,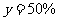 ;
;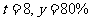 .
.
(1) 试确定该项学习任务的“学习曲线”;
(2) 计算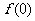 并指出其实际含义;
并指出其实际含义;
(3) 若定义在区间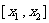 上的平均学习效率为
上的平均学习效率为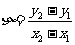 ,问这项学习任务从哪一时刻开始的2个单位时间内平均效率最高.
,问这项学习任务从哪一时刻开始的2个单位时间内平均效率最高.
[解] (1)
(2)
(3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com