
3.设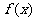 是可导函数,且
是可导函数,且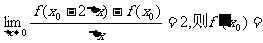
A.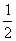 B.-1 C.0 D.-2
B.-1 C.0 D.-2
1 若集合
若集合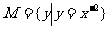 ,
,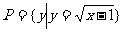 ,那么
,那么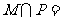
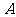

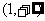
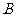

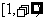
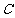

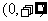
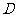

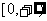
2.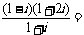
A.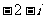 B.
B.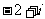 C.
C.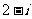 D.
D.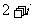
22.(本题满分14分)
设函数f(x)=(1+x)2-ln(1+x)2.
(1)求f(x)的单调区间;
(2)若当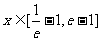 时,不等式f(x)<m恒成立,求实数m的取值范围;
时,不等式f(x)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=x2+x+a在区间[0,2]上恰好有两个相异的实根,求实数a的取值范围.
21.(本题满分12分)
以O为原点,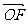 所在直线为x轴,建立如图所示的直角坐标系,设
所在直线为x轴,建立如图所示的直角坐标系,设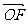 ·
·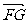 =1,点F的坐标为(t,0),
=1,点F的坐标为(t,0),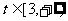 ,点G的坐标为(x0,y0).
,点G的坐标为(x0,y0).
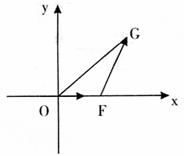 (1)求x0关于t的函数x0=f(t)的表达式,
(1)求x0关于t的函数x0=f(t)的表达式,
判断函数f(t)的单调性,并证明你的
判断;
(2)设△OFG的面积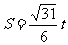 ,若以O
,若以O
为中心, F为焦点的椭圆经过点G,
求当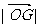 取最小值时椭圆的方程.
取最小值时椭圆的方程.
20.(本题满分12分)
我国加入WTO后,根据达成的协议,若干年内某产品关税与市场供应量P的关系允许近似的满足:
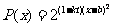 (其中t为关税的税率,且
(其中t为关税的税率,且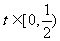 ).
).
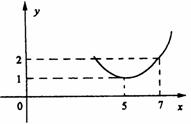 (x为市场价格,b、k为正常数),当t=
(x为市场价格,b、k为正常数),当t=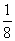 时的市场供应量曲线如图
时的市场供应量曲线如图
(1)根据图象求k、b的值;
(2)若市场需求量为Q,它近似满足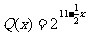 .
.
当P=Q时的市场价格称为市场平衡价格.为使市
场平衡价格控制在不低于9元,求税率t的最小
值.
19.(本题满分12分)
已知数列{an}中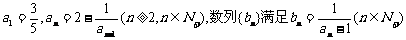 .
.
(1)求证数列{bn}是等差数列;
(2)求数列{an}中的最大项与最小项,并说明理由;
(3)记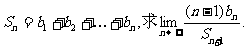
18.(本题满分12分)
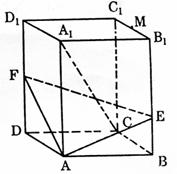 在长方体ABCD-A1B1C1D1中,E、F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
在长方体ABCD-A1B1C1D1中,E、F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
(1)求证:A1C⊥平面AEF;
(2)若AB=3,AD=4,AA1=5,M是B1C1
的中点,求AM与平面AEF所成角的大小;
(3)在(2)的条件下,求三棱锥D-AEF的体积.
17.(本题满分12分)
已知实数a,b,c成等差数列,a+1 , b+1, c+4成等比数列,求a, b,c.
16.对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②通径为8;
③过焦点的直线与抛物线交于两点的横坐标之积为4;
④抛物线上横坐标为2的点到焦点的距离为6;
⑤过焦点的弦中点坐标为(18,8).
能满足抛物线y2=8x的条件是 (填序号).
14.已知随机变量ξ的分布列为:
|
ξ |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
P |
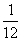 |
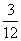 |
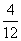 |
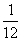 |
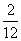 |
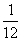 |
若P(ξ2<x)=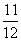 ,则实数x的取值范围是 .
,则实数x的取值范围是 .
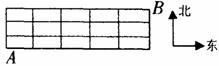 15.如图,小赵从A出发到达B处,他只知道
15.如图,小赵从A出发到达B处,他只知道
B在A的东北方向,图中一短线表示一段
道路,他每到一个交叉点路口时,对路线
作一次选择,每次都以概率P选择向东走,
以概率(1-p)选择向北走,经过8次选
择可到达B处的概率是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com