
4.(06年全国Ⅱ文科)已知集合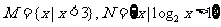 ,则
,则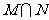 为
为
A.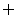 B.
B. C.
C.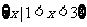 D.
D.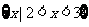
3.下列各式中最小值是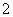 的是
的是
A.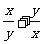 B.
B.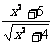 C.
C.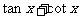 D.
D. 
2.(04年浙江文科)若U= {1,2,3,4}, M= {1,2}, N= {2,3}, 则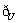 (M
(M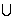 N) =
N) =
A. {1,2,3} B. {4} C.{1,3,4} D. {2}
1.已知集合P =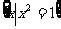 ,Q =
,Q =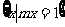 ,若Q
,若Q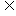 P,则实数m的值为
P,则实数m的值为
A. 1 B. 1,-1 C.-1 D. 0,1,-1
21. (14分) 设函数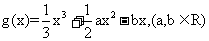 在其图象上一点P(x,y)处的切线的斜率记为f(x).
在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)讨论函数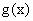 的极值的个数。
的极值的个数。
(2)若方程f(x)=0有两个实根分别为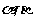 ,且
,且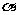 =
=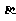 +1,求
+1,求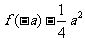 的值。
的值。
(3)若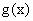 在区间
在区间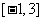 上是单调递减函数,求
上是单调递减函数,求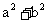 的最小值。
的最小值。
20.(13分)已知函数f(x)=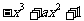 ,x∈[0,1].
,x∈[0,1].
(1)若f(x)在[0,1]上是增函数,求实数a的取值范围;
(2)求f(x)在[0,1]上的最大值.
19. (12分)设某物体一天中的温度T是时间t的函数,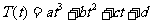 ,
,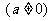 其中温度的单位是
其中温度的单位是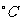 ,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8
,时间的单位是小时。t=0表示12:00, t取正值表示12:00点以后。若测得该物体在8:00的温度为8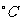 ,12:00的温度为60
,12:00的温度为60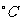 ,13:00的温度为58
,13:00的温度为58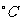 ,且已知该物体的温度在8:00和16:00有相同的变化率。
,且已知该物体的温度在8:00和16:00有相同的变化率。
(1)写出该物体的温度T关于时间t的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00,14:00)何时温度最高?并求出最高温度。
18.
(12分)已知曲线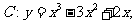 过原点存在两条直线与曲线C相切,
过原点存在两条直线与曲线C相切,
试求这两条直线方程。
17. (12分)已知函数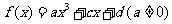 是R上的奇函数,当
是R上的奇函数,当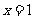 时,
时,
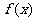 取得极值
取得极值 ,求
,求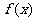 的单调递增区间和极大值。
的单调递增区间和极大值。
16.( 12分) 对50台电子设备的
寿命逐台进行测试,得到下列数据表:
|
范围 |
频数 |
 频率 频率 |
|
(0,500] |
16 |
|
|
(500,1000] |
14 |
|
|
(1000,1500] |
10 |
|
|
(1500,2000] |
6 |
|
|
(2000,2500] |
2 |
|
|
(2500,3000] |
0 |
|
|
(3000,3500] |
1 |
|
|
(3500,4000] |
1 |
 |
|
合计 |
50 |
|
(1)完成上面的表;
(2)画出频率分布直方图;
(3)根据所得结果估计,寿命小于2500 h的概率约是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com