
22.(本不题满分14分)已知定点F(1,0),动点P在y轴上运动,过点P做PM交x轴于点M,并延长MP到点N,且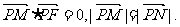
(Ⅰ)求点N的轨迹方程;
(Ⅱ)直线l与点N的轨迹交于A、B不同两点,若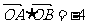 ,且
,且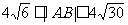 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
21.(本小题满分12分)已知函数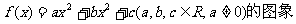
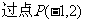 ,且在点P处的切线与直线
,且在点P处的切线与直线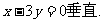
(Ⅰ)若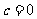 ,试求函数
,试求函数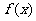 的单调区间;
的单调区间;
(Ⅱ)若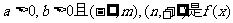 的单调递增区间,试求
的单调递增区间,试求 的范围.
的范围.
20.(本小题满分12分)高二(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功的概率为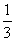 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.
(Ⅰ)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次发芽成功的概率;
(Ⅱ)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但实验的次数最多不超过5次,求第二小组所做种子发芽试验的次数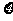 的概率分布列和数学期望.
的概率分布列和数学期望.
19.(本小题满分12分)如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
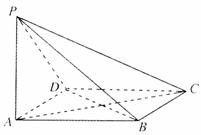 (Ⅰ)求证:平面PBD⊥平面PAC;
(Ⅰ)求证:平面PBD⊥平面PAC;
(Ⅱ)求点A到平面PBD的距离;
(Ⅲ)求二面角A-PB-D的余弦值.
18.(本小题满分12分)已知二次函数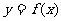 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为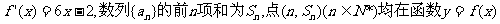 的图象上.
的图象上.
(Ⅰ)求数列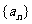 的通项公式;
的通项公式;
(Ⅱ)设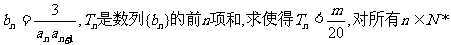 都成立的最小正整数m.
都成立的最小正整数m.
17.(本小题满分12分)已知函数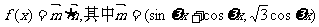 ,
,
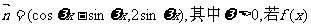 相邻两对称轴间的距离小于
相邻两对称轴间的距离小于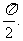
(Ⅰ)求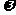 的取值范围;
的取值范围;
(Ⅱ)在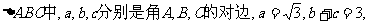
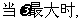
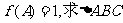 的面积.
的面积.
16.给出下列四个命题:
①存在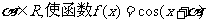 是奇函数;
是奇函数;
②要得到函数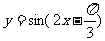 的图象,只要将函数
的图象,只要将函数 个单位;
个单位;
③函数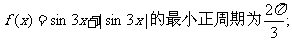
④函数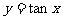 的图象既是中心对称图形,又是轴对称图形.
的图象既是中心对称图形,又是轴对称图形.
其中,真命题的编号是 .(写出所有真命题的编号)
15.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有: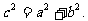
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用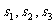 表示三个侧面面积,
表示三个侧面面积,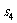 表示截面面积,那么你类比得到的结论是
.
表示截面面积,那么你类比得到的结论是
.
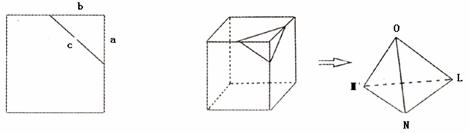
14.一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为 .
13.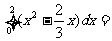 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com