
7. 一植物园参观路径如右图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
一植物园参观路径如右图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
A.6种 B.8种
C.36种 D.48种
6.已知a,b是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题:
①若a⊥α,a⊥β,则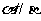 ②若
②若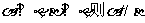
③若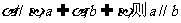 ④若
④若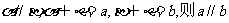
其中正确命题的序号是 ( )
A.①② B.①③ C.③④ D.①④
5.函数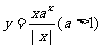 的图象的大致形状是 ( )
的图象的大致形状是 ( )
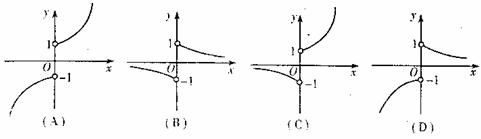
4.函数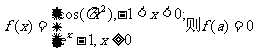 ,则a的所有可能值组成的集合为( )
,则a的所有可能值组成的集合为( )
A.{0} B.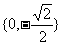
C.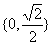 D.
D.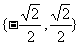
3.如果一个空间几何体的主视图与左视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为 ( )
A.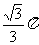 B.
B.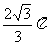 C.
C.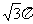 D.
D.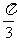
1.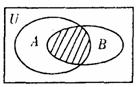 设全集
设全集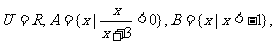 则右
则右
图中阴影部分表示的集合为 ( )
A.{x|x>0} B.
C.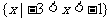 D.
D.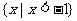
|
A.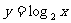 B.y=cosx C.
B.y=cosx C.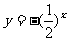 D.
D.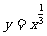
22.(本小题满分14分)
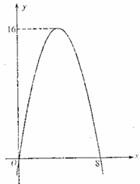
已知二次函数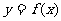 的图象如图所示.
的图象如图所示.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)在区间 ;
;
 (Ⅲ)若
(Ⅲ)若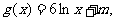 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
21.有一幅椭圆型彗星轨道图,长4cm,高 ,如下图,已知O为椭圆中心,A1,A2是长轴两端点,太阳位于椭圆的左焦点F处.
,如下图,已知O为椭圆中心,A1,A2是长轴两端点,太阳位于椭圆的左焦点F处.
(Ⅰ)建立适当的坐标系,写出椭圆方程,并求出当彗星运行到太阳正上方时二者在图上的距离;
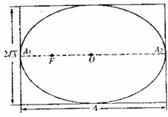 (Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,设P是l上异于D点的任意一点,直线A1P,A2P分别交椭圆于M、N(不同于A1,A2)两点,问点A2能否在以MN为直径的圆上?试说明理由.
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,设P是l上异于D点的任意一点,直线A1P,A2P分别交椭圆于M、N(不同于A1,A2)两点,问点A2能否在以MN为直径的圆上?试说明理由.
20.(本小题满分12分)
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1 ,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(Ⅰ)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(Ⅱ)年销售量关于x的函数为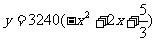 ,则当x为何值时,本年度的年利润最大?最大利润为多少?
,则当x为何值时,本年度的年利润最大?最大利润为多少?
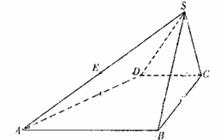
19.(本小题满分12分)
四棱锥S-ABCD的底面是直角梯形,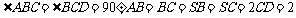 ,侧面SBC⊥底面ABCD
,侧面SBC⊥底面ABCD
(Ⅰ)由SA的中点E作底面的垂线EH,试确定垂足H的位置;
(Ⅱ)求二面角E-BC-A的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com