
1.已知集合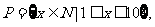 集合
集合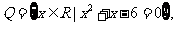 则
则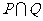 等于 ( )
等于 ( )
(A)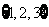 (B)
(B)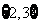 (C)
(C)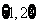 (D)
(D)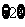
21、(本小题满分15分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
设不等式组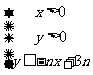 所表示的平面区域为Dn ,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n
所表示的平面区域为Dn ,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n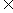 N*).
N*).
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)记Tn=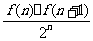 ,若对于一切正整数n,总有Tn≤m,求实数m的取值范围;
,若对于一切正整数n,总有Tn≤m,求实数m的取值范围;
(3)设Sn为数列{bn}的前n项和,其中bn=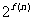 ,问是否存在正整数n、t,使
,问是否存在正整数n、t,使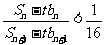 成立?若存在,求出正整数n , t;若不存在,说明理由.
成立?若存在,求出正整数n , t;若不存在,说明理由.
20.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
在直角坐标系中,O为坐标原点,设直线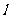 经过点
经过点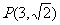 ,且与
,且与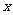 轴交于点
轴交于点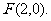
(I)求直线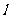 的方程;
的方程;
(II)如果一个椭圆经过点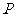 ,且以点
,且以点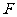 为它的一个焦点,求椭圆的标准方程;
为它的一个焦点,求椭圆的标准方程;
(III)若在(I)、(II)、情形下,设直线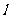 与椭圆的另一个交点为
与椭圆的另一个交点为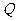 ,且
,且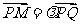 ,当
,当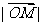 最小时,求
最小时,求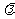 对应的值。
对应的值。
18、(本小题满分14分,第一小问满分6分,第二小问满分8分)
一个口袋内装有大小相同且已编有不同号码的4个黑球和3个红球,某人一次从中摸出2个球。
(I)如果摸到的球中含有红球就中奖,那么此人中奖的概率是多少?
(II)如果摸到的两个球都是红球,那么就中大奖。在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
 19、(本小题满分15分,第一小问满分5分,第二小问满分5分,第三小问满分5分)
19、(本小题满分15分,第一小问满分5分,第二小问满分5分,第三小问满分5分)
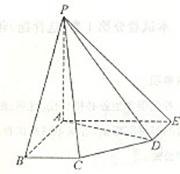
在五棱锥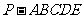 中,
中,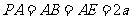 ,PB=PE
,PB=PE
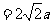 , BC=DE=
, BC=DE=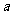 ,
,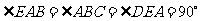 。
。
(I)求证: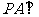 平面
平面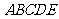 ;
;
(II)求二面角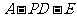 的大小。
的大小。
(III)求点C到平面PDE的距离。
17、(本小题12分,第一、二两小问满分各6分)
已知数列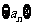 是等差数列,
是等差数列,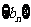 是等比数列,且
是等比数列,且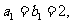
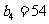 ,
, 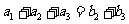 ,(I)求数列
,(I)求数列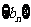 的通项公式;(II)求数列
的通项公式;(II)求数列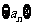 的前10项和
的前10项和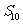 。
。
16、已知抛物线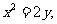 过点
过点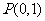 的直线与抛物线相交于
的直线与抛物线相交于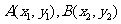 两点,则y1+y2的最小值是
。
两点,则y1+y2的最小值是
。
15、一个正四棱柱的顶点都在球面上,底面边长为1,高为2,则此球的表面积为
14、甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,且a,b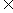 {0,1,2,3,…,9},若|a-b|≤1,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 .
{0,1,2,3,…,9},若|a-b|≤1,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 .
13、已知圆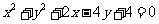 关于直线
关于直线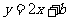 成轴对称,则
成轴对称,则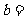 .
.
12、已知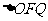 的面积为S,
的面积为S,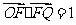 ,若
,若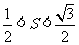 ,则向量
,则向量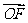 与
与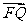 的夹角的范围是 .
的夹角的范围是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com