
1、直线x=-1与直线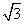 x+y=0的夹角为:
x+y=0的夹角为:
A.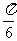 B.
B. 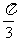 C.
C. 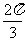 D.
D. 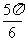
21.(本题满分16分)
已知数列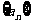 中,
中,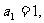 且点
且点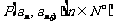 在直线
在直线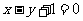 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)若函数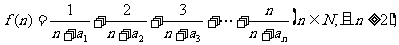 求函数
求函数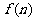 的最小值;
的最小值;
(3)设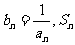 表示数列
表示数列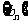 的前项和。试问:是否存在关于
的前项和。试问:是否存在关于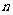 的整式
的整式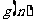 ,使得
,使得
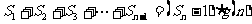 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
20.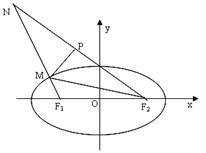 (本题满分14分) 如图已知F1、F2为椭圆
(本题满分14分) 如图已知F1、F2为椭圆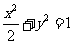 的两焦点,M是椭圆上一点,延长F1M到N,P是NF2上一点,且满足
的两焦点,M是椭圆上一点,延长F1M到N,P是NF2上一点,且满足
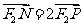 ,
,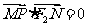 ,点N的轨迹方程为E。
,点N的轨迹方程为E。
⑴求曲线E的方程;
⑵过F1的直线l交椭圆于G,交曲线E于H,(G、H都在x轴上方),若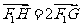 ,
,
求直线l的方程;
19.(本题满分14分)
如图,一个水轮的半径为4 m,水轮圆心O距离水面4 m,已在水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点p0)开始计算时间.
(1)将点p距离水面的高度z(m)表示为时间t(s)的函数;
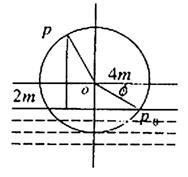 (2)点p第一次到达最高点大约需要多少时间?
(2)点p第一次到达最高点大约需要多少时间?
18. (本小题满分14分)
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=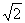 ,PB⊥PD.
,PB⊥PD.
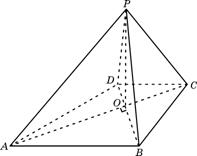 (Ⅰ)求异面直接PD与BC所成角的余弦值;
(Ⅰ)求异面直接PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且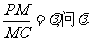 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
17.(本题12分)某人抛掷一枚硬币,出现正反的概率都是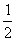 ,构造数列
,构造数列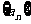 ,使得
,使得 ,记
,记 。
。
(1) 求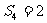 的概率;(2)若前两次均出现正面,求
的概率;(2)若前两次均出现正面,求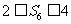 的概率。
的概率。
16. 如果函数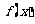 满足:对任意实数
满足:对任意实数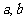 都有
都有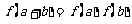 ,且
,且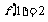 ,则
,则 ______________________.
______________________.
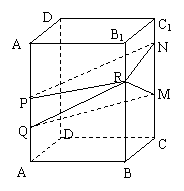
15.正四棱柱ABCD–A1B1C1D1中,
AB=3,BB1=4.长为1的线段PQ
在棱AA1上移动,长为3的线段
MN在棱CC1上移动,点R在棱
BB1上移动,则四棱锥R–PQMN
的体积是
14. 关于
关于 的方程
的方程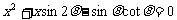 的两根为
的两根为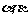 ,且
,且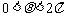 ,若数列
,若数列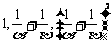 ,
,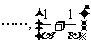 的前100项和为0,则
的前100项和为0,则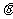 的值为
的值为
13.在数列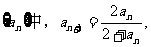 对任意正整数n都成立,且
对任意正整数n都成立,且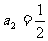 ,则
,则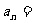 _______________
_______________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com