
19.(本题满分12分)
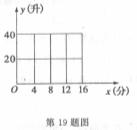
某种洗衣机洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时问为2
分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
|
x |
0 |
2 |
4 |
16 |
17 |
18 |
… |
|
y |
0 |
20 |
40 |
40 |
|
2 |
… |
请根据表中提供的信息解答下列问题:
(1)试写出当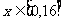 时,y关于x的函数解析式,并画出该函数的图像;
时,y关于x的函数解析式,并画出该函数的图像;
(2)根据排水阶段点(x,y)的分布情况,可选用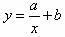 或
或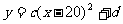 。 (其中a、b、c、d为常数)
。 (其中a、b、c、d为常数)
作为排水阶段洗衣机中的水量Y与时间X之间关系的模拟函数.
试分别求出这两个函数的解析式,并预测17分钟时洗衣机中的水量(精确到1升).
18.(本题满分12分)
已知定义域为R的函数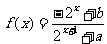 是奇函数.
是奇函数.
(1)求a,b的值。
(2)若对任意的t∈R,不等式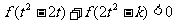 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
17.(本题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(1)求角B的大小;
(2)设向量m=(sinA,cos2A),n=(4k,1)(k>1), m·n的最大值为5,求k的值.
16.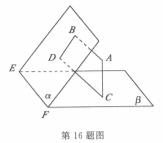 如图,设平面
如图,设平面 垂足分别为B、D.若增加一个条件,就能推出
垂足分别为B、D.若增加一个条件,就能推出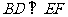 .现有:
.现有:
①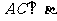 ;
;
②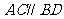 ;
;
③AC与CD在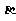 内的射影在同一条直线上;
内的射影在同一条直线上;
④
那么上述几个条件中能成为增加条件的是______ (填上你认为正确的所有答案序号).
15.在平面内,三角形的面积为s,周长为C,则它的内切圆的半径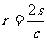 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=________.
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=________.
14. 已知向量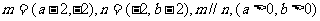 ,则ab的最小值是_____
,则ab的最小值是_____
13.已知函数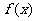 是定义在
是定义在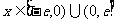 上的奇函数,当
上的奇函数,当
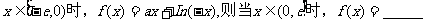
12.同时满足条件①函数图像成中心对称图形;②对任意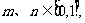 若m≠n,有
若m≠n,有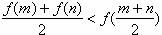 的函数是
的函数是
(A)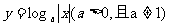 (B)y=cos2x
(B)y=cos2x
(C) 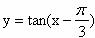 (D)
(D)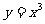
第Ⅱ卷 (非选择题 共90分)
11.已知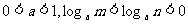 ,则
,则
(A)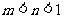 (B)
(B)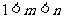
(C) 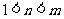 (D)
(D)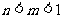
10.直线L: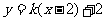 与圆C:
与圆C: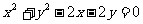 相切,则直线L的一个方向向量等于
相切,则直线L的一个方向向量等于
(A)(1,-1) (B)(1,1) (C)(-3,2) (D)(1,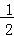 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com