
2.直线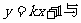 曲线
曲线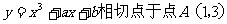 ,则b的值为
,则b的值为
A.3 B.-3 C.2 D.-2
1.已知集合M={y|y=x2+2x+2,x∈R},集合N={x|y=log2(4-x),y∈R},则集合M∩N为
A.(2,+∞) B.(-∞,3) C.(1,3) D.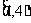
(17)(本小题满分12分)在等比数列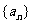 中,
中,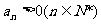 ,公比
,公比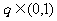 ,且
,且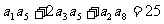 ,又
,又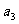 与
与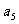 的等比中项为
的等比中项为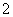 ,
,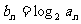 ,数列
,数列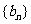 的前
的前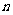 项和为
项和为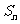 。
。
(1)求数列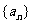 的通项公式。
的通项公式。
(2)求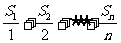 最大值?
最大值?
 (18)(本小题满分14分)如图,正方形
(18)(本小题满分14分)如图,正方形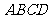 、
、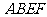 的边长都是1,而且平 面
的边长都是1,而且平 面 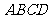 、
、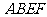 互相垂直。点
互相垂直。点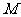 在
在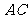 上移动,点
上移动,点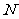 在
在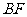 上移动,若
上移动,若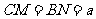 (
(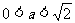 )
)
(I)求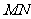 的长;
的长;
(II)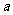 为何值时,
为何值时,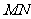 的长最小;
的长最小;
(III)当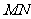 的长最小时,求面
的长最小时,求面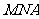 与面
与面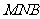 所成二面角
所成二面角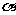 的大小。
的大小。
(19)(本小题满分14分)已知直线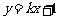 与双曲线
与双曲线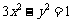 有A、B两个不同的交点.
有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线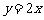 对称?试述理由.
对称?试述理由.
.
(20)(本小题满分14分)已知函数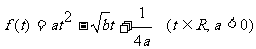 的最大值为正实数,集合
的最大值为正实数,集合
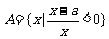 ,集合
,集合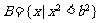 。
。
(1)求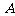 和
和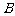 ;
;
(2)定义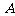 与
与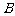 的差集:
的差集: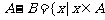 且
且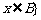 。
。
设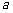 ,
,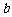 ,
,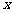 均为整数,且
均为整数,且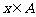 。
。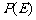 为
为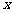 取自
取自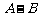 的概率,
的概率,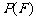 为
为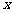 取自
取自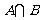 的概率,写出
的概率,写出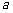 与
与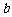 的二组值,使
的二组值,使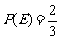 ,
,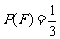 。
。
(3)若函数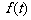 中,
中,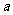 ,
,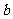 是(2)中
是(2)中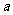 较大的一组,试写出
较大的一组,试写出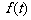 在区间[
在区间[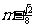 ,
,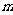 ]上的最大值函数
]上的最大值函数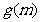 的表达式。
的表达式。
(21)(本小题满分16分)设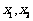 是函数
是函数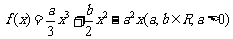 的两个极值点,
的两个极值点,
且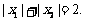
(I)证明: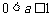 ;
;
(II)证明: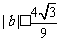 ;
;
(III)若函数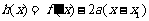 ,证明:当
,证明:当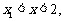 且
且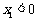 时,
时,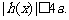
(11)、在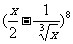 的展开式中常数项是________.
的展开式中常数项是________.
(12)、已知点P(1,2)在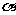 终边上,则
终边上,则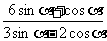 =
。
=
。
(13)、在△OAB中,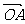 =(2cosα,2sinα),
=(2cosα,2sinα),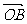 =(5cosβ,5sinβ),若
=(5cosβ,5sinβ),若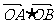 =-5,则S△OAB= ________.
=-5,则S△OAB= ________.
(14)、已知有向线段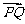 的起点
的起点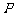 和终点
和终点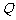 的坐标分别为
的坐标分别为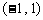 和
和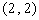 ,若直线
,若直线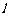 :
: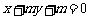 与线段
与线段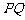 相交,则
相交,则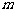 的取值范围是 。
的取值范围是 。
(15)、已知关于x的不等式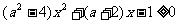 的解集是空集,求实数a的取值范围
。
的解集是空集,求实数a的取值范围
。
(16)、已知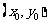 是
是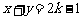 与圆
与圆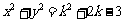 的公共点,则当
的公共点,则当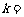
时, 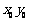 最小.
最小.
(1)已知集合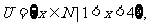 集合
集合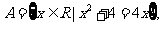 则
则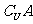 等于( )
等于( )
(A)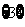 (B)
(B)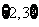 (C)
(C)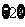 (D)
(D)
(2)函数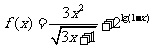 的定义域是( )
的定义域是( )
A.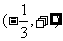 B.
B. 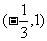 C.
C. 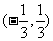 D.
D.
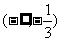
(3)函数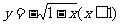 的反函数是( )
的反函数是( )
A、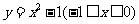 B、
B、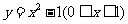
C、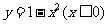 D、
D、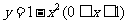
(4)、若抛物线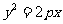 的焦点与双曲线
的焦点与双曲线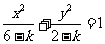 的右焦点重合,则
的右焦点重合,则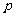 的值为( )
的值为( )
A. B.
B.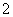 C.
C. D.
D.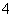
(5)、若f(sin2x)=3-cos2x,则f(cosx)的最小正周期是 ( )
(A)2π (B)4π (C) (D)π
(6)、已知数列{an},首项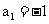 ,它的前n项和为Sn,若
,它的前n项和为Sn,若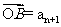
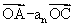 ,且A、B、C三点共线(该直线不过原点O),则S20=( )
,且A、B、C三点共线(该直线不过原点O),则S20=( )
A.170 B. 101 C.200 D.210
(7)、在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶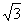 B.1∶9 C.1∶
B.1∶9 C.1∶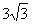 D.1∶
D.1∶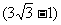
(8)、2005年底,某地区经济调查队对本地区居民收入情况进行抽样调查,抽取1000户,按
|
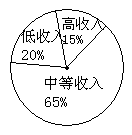 本地区确定的标准,情况如右表:
本地区确定的标准,情况如右表:
本地区在“十一五”规划中明确
提出要缩小贫富差距,到2010年
要实现一个美好的愿景,由右边圆图显示,则中等收入家庭的数
量在原有的基础要增加的百分比和低收入家庭的数量在原有的基
础要降低的百分比分别为 ( )
A.25% , 27.5% B.62.5% , 57.9% C.25% , 57.9% D.62.5%,42.1%
(9)、如下图,已知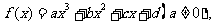 记
记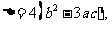 则当
则当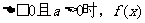 的大致图像为( ).
的大致图像为( ).
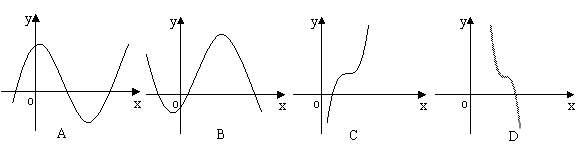 (10)、已知
(10)、已知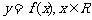 是奇函数,且
是奇函数,且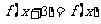 恒成立,又
恒成立,又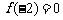 ,则方程
,则方程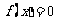 在
在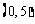 内解的个数的最小值为( ).
内解的个数的最小值为( ).
A.4 B.5 C.6 D.7
第Ⅱ卷
(本卷共100分)
21.(本小题满分15分) 已知函数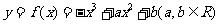 。
。
(1)要使 在(0,1)上单调递增,试求
在(0,1)上单调递增,试求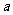 的取值范围;
的取值范围;
(2)当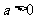 时,若函数满足
时,若函数满足 ,试求函数
,试求函数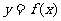 的解析式;
的解析式;
(3)若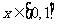 时,
时,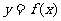 图象上任意一点处的切线倾斜角为
图象上任意一点处的切线倾斜角为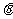 ,求当
,求当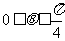 时
时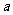 的取值范围。
的取值范围。
20.(本小题满分15分)设Sn是数列 的前n项和,且
的前n项和,且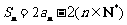 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 使
使
 ,求
,求 的通项公式;
的通项公式;
(3)设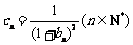 ,且数列
,且数列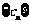 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与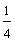 的大小.
的大小.
19.(本小题满分14分)已知圆M: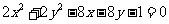 和直线
和直线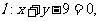 过直线 上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上.
过直线 上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上.
(1)当A的横坐标为4时,求直线AC的方程;
(2)求点A的横坐标的取值范围.
18.(本小题满分14分)已知函数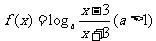 .
.
(1)求 的定义域,并判断
的定义域,并判断 的奇偶性;
的奇偶性;
(2)解关于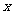 的不等式:
的不等式: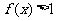 .
.
17.(本小题满分12分)已知 .
.
⑴.求证: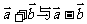 互相垂直;
互相垂直;
⑵.若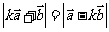 ,求
,求 (其中k为非零实数).
(其中k为非零实数).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com