
3.若a>0,b>0,则不等式-b<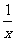 <a等价于( )
<a等价于( )
A.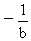 <x<0或0<x<
<x<0或0<x<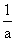 B.-
B.-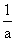 <x<
<x<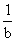
C.x<-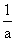 或x>
或x>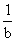 D.x<
D.x<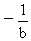 或x>
或x>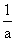
2.“a>0,b>0”是“ab>0”的( )
A. 充分而不必要条件 B. 要而不充分条件
C. 分必要条件 D. 允分也不必要条件
1.不等式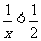 的解集是( )
的解集是( )
A.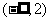 B.
B. C.
C.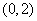 D.
D.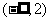
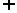

22.(本小题满分14分)
椭圆G: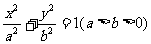 的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足
的两个焦点F1(-c,0)、F2(c,0),M是椭圆上的一点,且满足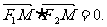
(Ⅰ)求离心率e的取值范围;
(Ⅱ)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为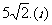 求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点
求此时椭圆G的方程;(ⅱ)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点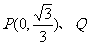 的直线对称?若能,求出k的取值范围;若不能,请说明理由.
的直线对称?若能,求出k的取值范围;若不能,请说明理由.
|
21.(本小题满分12分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(Ⅰ)试解释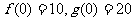 的实际意义;
的实际意义;
(Ⅱ)设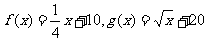 ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
20.(本小题满分12分)
设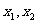 是函数
是函数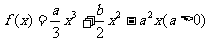 的两个极值点,且
的两个极值点,且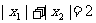
(Ⅰ)求a的取值范围;
(Ⅱ)求证: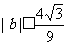 .
.
19.(本小题满分12分)
已知数列{an}的前n项和为Sn,且满足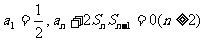
(Ⅰ)判断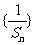 是否为等差数列?并证明你的结论;
是否为等差数列?并证明你的结论;
(Ⅱ)求Sn和an
|
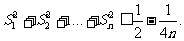
18.(本小题满分12分)
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2和1.
(Ⅰ)求证: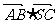 是定值;
是定值;
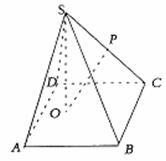 (Ⅱ)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长,若不存在,请说明理由.
(Ⅱ)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长,若不存在,请说明理由.
17.(本小题满分12分)
已知a、b、c是△ABC三边长,关于x的方程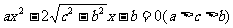 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积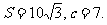
(Ⅰ)求角C;
(Ⅱ)求a、b的值.
16.已知函数f(x)满足: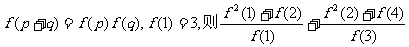 +
+
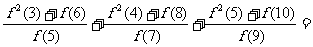 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com