
2. 要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为( )
A.5个 B.10个 C.20个 D.45个
1.已知集合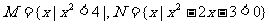 ,则集合
,则集合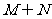 =( )
=( )
A.{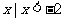 } B.{
} B.{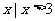 }
}
C.{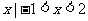 } D. {
} D. {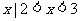 }
}
21.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,且f '(1)=0.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设数列{an}满足条件:a1∈(1,2),an+1=f (an)
求证:(a1- a2)·(a3-1)+(a2- a3)·(a4-1)+…+(an- an+1)·(an+2-1)<1
20.(本小题满分16分,第一小问5分,第二小问满分5分,第三小问满分6分)
对于函数y=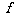 (
(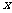 )(
)( 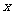
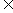 D,D为函数定义域),若同时满足下列条件:
D,D为函数定义域),若同时满足下列条件:
① f(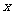 )在定义域内单调递增或单调递减;
)在定义域内单调递增或单调递减;
②
存在区间[a ,b]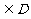 ,使
,使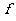 (
(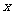 )在[a ,b]上的值域是[a
,b]。
)在[a ,b]上的值域是[a
,b]。
那么把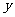 =
= 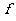 (
(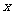 )(x
)(x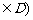 称为闭函数.
称为闭函数.
(Ⅰ) 求闭函数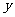 = –
= –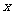 3符合条件②的区间[a,b];
3符合条件②的区间[a,b];
(Ⅱ)判定函数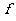 (
(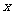 )=
)= 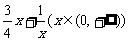 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(Ⅲ) 若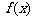 =
=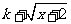 是闭函数,求实数
是闭函数,求实数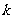 的取值范围
的取值范围
19.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
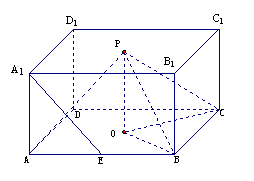
如图,O,P分别是正四棱柱ABCD-A1B1C1D1底面中心,E是AB的中点,AB=kAA1,
(Ⅰ)求证:A1E∥平面PBC;
(Ⅱ)当k=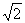 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
18.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c在点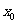 处取得极小值-5,其导函数
处取得极小值-5,其导函数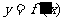
的图象经过点(0,0),(2,0),
(Ⅰ)求a,b的值;
(Ⅱ)求x0及函数f(x)的表达式。
17.(本小题满分12分)
设双曲线C: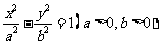 的离心率e=2,经过双曲线的右焦点F且倾斜角为60º的直线交双曲线于A、B点,若
的离心率e=2,经过双曲线的右焦点F且倾斜角为60º的直线交双曲线于A、B点,若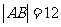 ,求此时的双曲线方程。
,求此时的双曲线方程。
16. 给出下列四个命题:
①过平面外一点,作与该平面成θ角的直线一定有无穷多条。
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为: ▲ 。
15.在△ABC中,cosB为sinA、sinC的等比中项,sinB为cosA、cosC的等差中项,则∠B= ▲ .
14.椭圆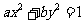 与直线
与直线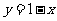 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为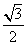 ,则 值 = ▲ .
,则 值 = ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com