
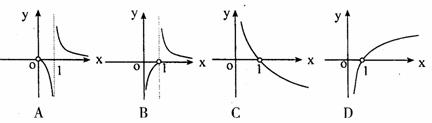
4.函数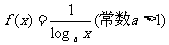 的大致图象是 ( )
的大致图象是 ( )
3.幂函数的图象过点(2,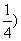 ,则它的单调递增区间是 ( )
,则它的单调递增区间是 ( )
A.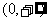 B.
B.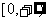 C.
C. D.
D.
2.下列命题中是全称命题并且是真命题的是 ( )
A.每个二次函数的图象开口都向上
B.对任意非正数c,若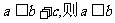
C.存在一条直线与两个相交平面都垂直
D.存在一个实数x使不等式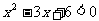 成立
成立
1.化简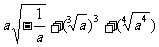 得 ( )
得 ( )
A.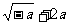 B.
B.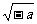 C.-
C.-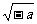 D.-
D.-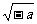 +2a
+2a
22.(本小题满分14分)已知函数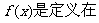 [-2,2]上的奇函数,当
[-2,2]上的奇函数,当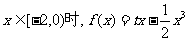 (t为常数).
(t为常数).
(1)求函数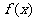 的解析式;
的解析式;
(2)当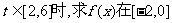 上的最小值以及取得最小值时的x值;
上的最小值以及取得最小值时的x值;
(3)当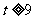 时,证明函数
时,证明函数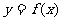 的图像至少有一个点落在直线
的图像至少有一个点落在直线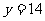 上.
上.
21.(本小题满分12分)设O点为坐标原点,曲线 ,满足关于直线
,满足关于直线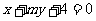 对称,又满足
对称,又满足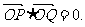
(1)求m的值;
(2)求直线PQ的方程.
20.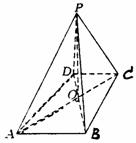 (本题满分12分)如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
(本题满分12分)如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=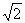 ,PB⊥PD.
,PB⊥PD.
(1)求异面直线PD与BC所成角的余弦值;
(2)求二面角P-AB-C的大小;
(3)设点M在棱PC上,且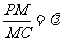 ,问
,问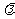 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
19.(本小题满分12分)在圆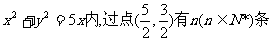 弦,它们的长构成等差数列,
弦,它们的长构成等差数列,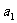 为过该点的最短的弦长,
为过该点的最短的弦长,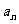 为过该点的最长的弦长,若公差
为过该点的最长的弦长,若公差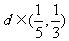 ,求n的值.
,求n的值.
18.(本小题满分12分)已知如图,AB是圆柱下底面圆O2的直径,PA是圆柱的一条母线,C是圆柱下底面圆O2圆周上一点.
(1)求证:BC⊥平面PAC;
(2)若C恰为弧AB的中点,按图中所给尺寸,计算三棱锥B-PAC的体积.
17.(本小题满分12分)已知函数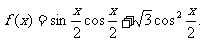
(1)求当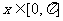 时,
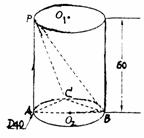
时,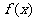 的零点; (2)求
的零点; (2)求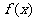 的值域;
的值域;
 (3)将
(3)将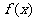 的图象经过怎样的平移,使得平移后的图象关于原点对称?(只需说出一种平移途径即可)
的图象经过怎样的平移,使得平移后的图象关于原点对称?(只需说出一种平移途径即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com