
1、定义集合A与B的新运算,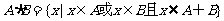 ,则
,则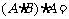 ( )
( )
A、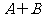 B、
B、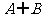 C、A D、B
C、A D、B
21.(14分)设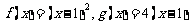 ,数列{an}满足
,数列{an}满足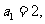
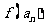
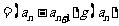 ,数列
,数列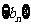 满足
满足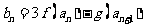
(1)证明 是等比数列;
是等比数列;
(2)设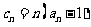 ,且
,且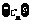 的前n项和为
的前n项和为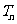 ,求
,求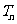 的表达式;
的表达式;
(3)求数列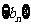 中
中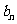 的最大值与最小值.
的最大值与最小值.
20.
(14分)某森林出现火灾,火势正以每分钟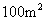 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火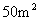 ,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.
,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.
(1)设派x名消防队员前去救火,用t分钟将火扑灭,试建立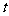 与
与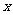 的函数关系式;
的函数关系式;
(2)问应该派多少消防队员前去救火,才能使总损失最少?
19. (14分)设Sn是数列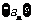 的前n项和,且
的前n项和,且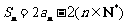 .
.
(1)求数列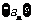 的通项公式;
的通项公式;
(2)若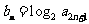 ,设
,设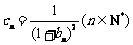 ,且数列
,且数列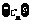 的前n项和为Tn ,证明:Tn<
的前n项和为Tn ,证明:Tn<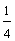 .
.
18. (14分)已知函数f(x)=ax3+bx2,曲线y=f(x)过点P(-1,2),且在点P处的切线恰好与直线x-3y=0垂直.
(1)求实数a ,b的值;
(2)若关于x的方程f(x)+k=0在[-3,2]上仅有一实数解,求实数k的取值范围.
17.
(12分) 记函数f(x)=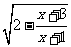 的定义域为A,g(x)=
的定义域为A,g(x)=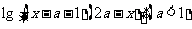 的定义域为B.
的定义域为B.
(1)求A;
(2)若B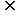 A ,求实数a的取值范围.
A ,求实数a的取值范围.
16.(12分)若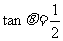 ,求
,求
15. 已知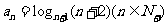 ,我们把使乘积a1·a2·a3·…·an为整数的数n叫做“劣数”,则在区间[1,2006]内的所有劣数的和为
,我们把使乘积a1·a2·a3·…·an为整数的数n叫做“劣数”,则在区间[1,2006]内的所有劣数的和为
14.设偶函数f(x)对任意x∈R,都有:f(x+3) =-f(x),且当x∈[-3,-2]时,f(x)=2x,则f(113.5)=
13.设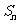 是等差数列
是等差数列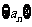 的前n项和,若公差
的前n项和,若公差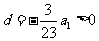 ,则使
,则使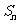 取最小值的正整数n的值是
取最小值的正整数n的值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com