
1.圆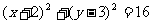 的圆心坐标和半径分别是 ( )
的圆心坐标和半径分别是 ( )
A.(2,3)和4 B.(2,-3)和4 C.(-2,3)和4 D.(-2,3)和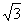
(17)(本小题满分12分)
设全集U=R,集合A={x|y=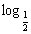 (x+3)(2-x)},B={x|
(x+3)(2-x)},B={x|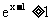 }.
}.
(I)求A∪B;
(Ⅱ)求( )∩B.
)∩B.
(18)(本小题满分12分)
已知直线l经过点P(-2,5),且斜率为-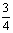 .
.
(I)求直线l的方程;
(II)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.
(19)(本小题满分12分)
如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,M、N分别为BB1、A1C1的中点.
(I)求证:AB⊥CB1
(Ⅱ)求证:MN∥平面ABC1
(20)(本小题满分12分)
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图I所示,日销售量Q(件)与时间f(天)之间的关系如下表所示.

(I)根据图I,写出该产品每件销售价格P与时间t的函数关系式;
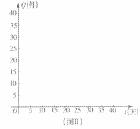 (Ⅱ)在所给的直角坐标系(图Ⅱ)中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销量Q与时间t的一个函数关系式;
(Ⅱ)在所给的直角坐标系(图Ⅱ)中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销量Q与时间t的一个函数关系式;
(Ⅲ)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)
(21)(本小题满分12分)
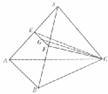 如图,在正三棱锥S-ABC中,E、F分别是侧棱SA、SB的中点,且平面CEF⊥平面SAB.
如图,在正三棱锥S-ABC中,E、F分别是侧棱SA、SB的中点,且平面CEF⊥平面SAB.
(I)若G为EF的中点,求证:CG上平面SAB;
(Ⅱ)求此三棱锥的侧面积与底面积的比值.
(22)(本小题满分14分)
定义在[-1,1]上的奇函数f(x),当-l≤x<0时f(x)=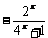 .
.
(I)求f(x)在[-1,1]上的解析式;
(Ⅱ)判断f(x)在(0,1)上的单调性,并给予证明;
(Ⅲ)当x∈(0,1]时,关于x的方程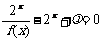 有解,试求实数
有解,试求实数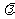 的取值范围.
的取值范围.
(13)已知幂函数y=f(x)的图象过点(2,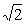 ),则f(9)=________.
),则f(9)=________.
(14)光线从点M(3,-2)射到y轴上一点P(0,1)后,被y轴反射,则反射光线所在直线的方程为__________.
(15)已知各顶点都在同一个球面上的正四棱柱高为4,体积为16,则这个球的体积为_______.
(16)已知函数f(x)=lnx,对于函数F(x)定义域中任意x1、x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)+f(x2)
②f(x1+x2)=f(x1)·f(x2)
③f(x1·x2)=f(x1)+f(x2)
④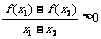
(1)A、B为数轴上的两点,A点坐标是-2,AB=5,那么B点坐标是
(A)3 (B)-7 (C)3或-7 (D)-3或7
(2)直线x+ay-7=O与直线(4a+1)x-y-6=0互相垂直,则a的值是
(A)-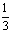 (B)
(B) 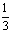 (C)-
(C)- 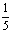 (D)
(D)
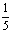
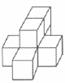 (3)如果用口表示一个正方体,用
(3)如果用口表示一个正方体,用 表示两个正方体叠加,用■表示三个正方体叠加,那么右图中的几何体(由7个正方体叠成),从正前方观察,可画出的平面图形是
表示两个正方体叠加,用■表示三个正方体叠加,那么右图中的几何体(由7个正方体叠成),从正前方观察,可画出的平面图形是

(4)已知集合S中的三个元素分别是△ABC的三边长,那么△ABC一定不是
(A)锐角三角形 (B)等腰三角形 (C)钝角三角形 (D)直角三角形
(5)点A(a+b,ab)在第一象限内,则直线bx+ay-ab=0不经过的象限是
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(6)函数f(x)= 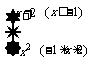 ,若f(x)=3,则x的值是
,若f(x)=3,则x的值是
(A)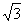 (B)±
(B)±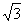 (c)1 (D)
(c)1 (D) 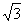 或1
或1
(7)若n=(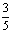 )x,6=x3,c=
)x,6=x3,c=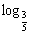 x,则当x>l时,a、b、c的大小关系是
x,则当x>l时,a、b、c的大小关系是
(A)a<b<c (B)c<b<a (C)c<a<b (D)a<c<b
(8)已知直线a、b和平面a、b,下列命题中错误的是
(A)若a∥b,a⊥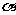 ,则b⊥
,则b⊥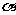 (B)若a⊥
(B)若a⊥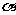 ,b⊥
,b⊥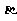 ,
,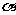 ∥
∥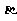 ,则a∥b
,则a∥b
(C)若a∥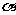 ,b∥
,b∥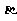 ,
,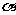 ∥
∥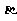 ,则a∥b (D)若a⊥
,则a∥b (D)若a⊥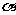 ,b⊥
,b⊥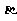 ,
,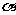 ⊥
⊥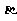 ,则a⊥b
,则a⊥b
(9)如果某林区的森林蓄积量每年平均比上年增长11.3%,经过x年可以增长到原来的 y倍,则函数y=f(x)的图象大致为

(10)一个正方体和一个圆柱等高,并且侧面积相等,则正方体与圆柱的体积比是
(A)∏:4 (B)4:∏ (C)1:1 (D) ∏2:4
(11)已知函数f(x)在R上为偶函数,当x∈[0,+∞)时,f(x)=x-1,则f(x)<0的解集是
(A)(-1,0) (B)(-1,1) (C)(O,1) (D)(-∞,-1)u(1,+∞)
(12)设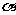 ∥
∥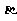 ,A∈
,A∈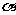 ,B∈
,B∈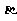 ,C是AB的中点,当A、B分别在平面
,C是AB的中点,当A、B分别在平面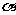 、
、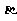 内运动时,那么所有动点C
内运动时,那么所有动点C
(A)不共面 (B)当且仅当A、B分别在两条平行直线上移动时才共面
(C)当且仅当A、B分别在两条给定的异面直线上移动时才共面
(D)不论A、B如何移动,都共面
第Ⅱ卷 (非选择题共90分)
(17)(本小题满分12分)
已知数列{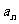 }是首项,
}是首项,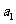 =4、公比
=4、公比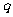 ≠1的等比数列,
≠1的等比数列,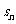 是其前n项和,且4
是其前n项和,且4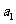 ,
,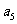 ,-2
,-2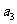 成等差数列.
成等差数列.
(I)求公比q的值;
(Ⅱ)求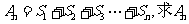 .
.
(18)(本小题满分12分))
已知函数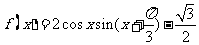
(I)求函数以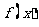 的最小正周期T;
的最小正周期T;
(Ⅱ)若△ABC的三边a,b,c满足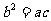 ,且边b所对的角为B,试求cosB的取值范围,并确定此时
,且边b所对的角为B,试求cosB的取值范围,并确定此时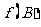 的最大值.
的最大值.
(19)(本小题满分12分)
某高等学校自愿献血的50位同学的血型分布情形如下表:
|
血型 |
A |
B |
AB |
O |
|
人数 |
20 |
10 |
5 |
15 |
(I)今从这50人中随机选出两人,问两人血型相同的概率是多少?
(Ⅱ)今有A血型的病人需要输血,从血型为A、O的同学中随机选出2人准备献血,记选择出A血型的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 ?
?
(20)(本小题满分12分)
一个多面体的直观图及三视图如图所示:(其中M、N别是AF、BC的中点).
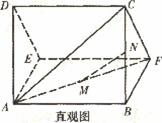 (I)求证:MN//平面CDEF;
(I)求证:MN//平面CDEF;
(Ⅱ)求二面角D-MN-B的余弦值绝对值.
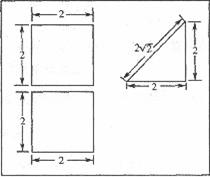
三视图
(21)(本小题满分12分)
如图,已知A、B、C是椭圆E: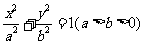 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为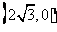 ,BC过椭圆的中心0,且AC⊥BC,
,BC过椭圆的中心0,且AC⊥BC,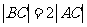 .
.
(I)求点C的坐标及椭圆E的方程;
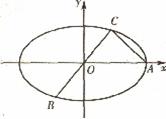 (Ⅱ)若椭圆E上存在两点P、Q,使∠PCQ的平分线总是垂直于x轴,试叛断向量
(Ⅱ)若椭圆E上存在两点P、Q,使∠PCQ的平分线总是垂直于x轴,试叛断向量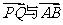 是否共线,并给出证明。
是否共线,并给出证明。
(22)(本小题满分14分)
已知函数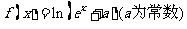 是实数集R上的奇函数,函数
是实数集R上的奇函数,函数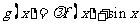 是区间[一1,1]上的减函数.
是区间[一1,1]上的减函数.
(I)求a的值;
(II) 若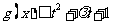 在x∈[一1,1]上恒成立,求t的取值范围.
在x∈[一1,1]上恒成立,求t的取值范围.
(Ⅲ) 讨论关于x的方程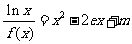 的根的个数。
的根的个数。
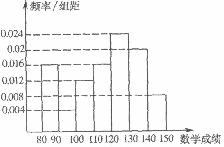 (13)已知二项式
(13)已知二项式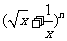 的展开式的第6项为常数项,则n=
的展开式的第6项为常数项,则n=
(14)在Rt△ABC中,∠C=90°,∠A=30°,则以A、B为焦点,过点C的椭圆的离心率是
(15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图).则这10000人中数学成绩在[140,150]段的约是 。
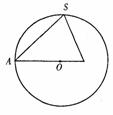 (16)已知三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为 .
(16)已知三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为 .
(1)复数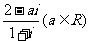 是纯虚数,则
是纯虚数,则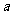 =
=
(A)0 (B)1 (C)2 (D)3
(2)抛物线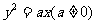 的焦点到其准线的距离是
的焦点到其准线的距离是
(A)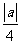 (B)
(B)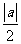 (c)
(c)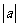 (D)
(D)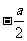
(3)用二分法研究函数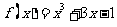 的零点时,第一次经计算
的零点时,第一次经计算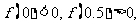 可得其中一个零点
可得其中一个零点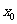 ∈ ,第二次应计算
.以上横线上应填的内容为
∈ ,第二次应计算
.以上横线上应填的内容为
(A)(0,0.5),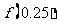 (B)(0,1),
(B)(0,1),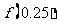
(C)(0.5,1),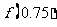 D)(0,0.5),
D)(0,0.5),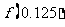
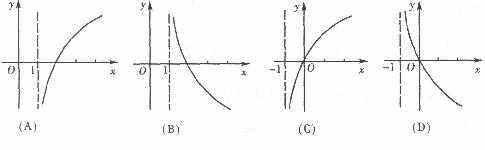
(4)若函数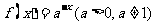 是定义域为R的增函数,则函数
是定义域为R的增函数,则函数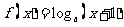 的图象大致是
的图象大致是
(5)已知a,b表示直线,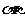 表示平面,则a∥
表示平面,则a∥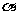 的一个充分条件是
的一个充分条件是
(A)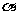 //
//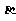 ,
,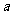 //
//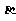 (B)
(B)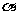 ⊥
⊥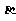 ,
,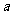 ⊥
⊥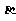
(C)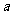 //
//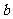 ,
,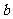 //
//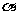 (D)
(D)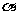
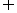
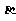 =
=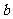 ,
,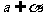 ,
,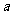 //
//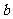
(6)过抛物线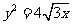 的焦点,且与圆
的焦点,且与圆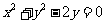 相切的直线方程是
相切的直线方程是
(A)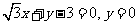
(B)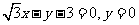
(C)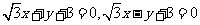
(D)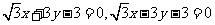
(7)已知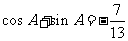 ,A为第四象限角,则ta
nA等于
,A为第四象限角,则ta
nA等于
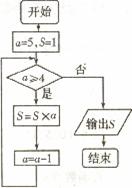 (A)
(A)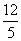 (B)
(B)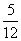 (C)
(C)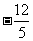 (D)
(D)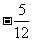
(8)右面的程序框图输出的结果是
(A)5
(B)10
(C)15
(D)20
(9)已知函数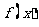 是以2为周期的偶函数,且当石
是以2为周期的偶函数,且当石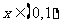 时,
时,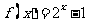 ,则
,则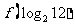 的值为
的值为
(A)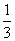 (B)
(B) 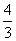 (C)2 (D)11
(C)2 (D)11
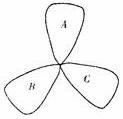 (10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(A)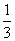 (B)
(B) 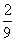
(C) 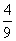 (D)
(D) 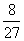
(11)已知等差数列{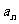 }的前n项和为
}的前n项和为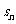 ,若
,若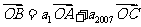 ,且A、B、C三点共线(0为该直线外一点),则
,且A、B、C三点共线(0为该直线外一点),则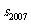 =
=
(A)2007 (B)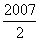 (C)
(C)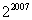 (D)
(D) 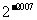
(12)点P是双曲线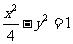 的右支上一点,M、N分别是圆
的右支上一点,M、N分别是圆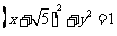 和圆
和圆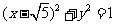 上的点,则
上的点,则 的最大值是
的最大值是
(A)2 (B)4 (C)6 (D)8
第Ⅱ卷 (非选择题共90分)
22.(本小题满分14分)如图,线段AB过点M(m,0),m为正数,且点A、B到x轴的距离之积为4m,抛物线C以x轴为对称轴,且过O、A、B三点(其中O为坐标原点).
(Ⅰ)求抛物线C的方程;
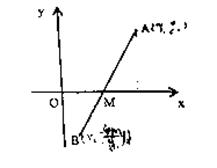 (Ⅱ)若
(Ⅱ)若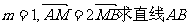 的方程.
的方程.
21.(本题满分14分)对实数a,b同义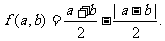
回答:
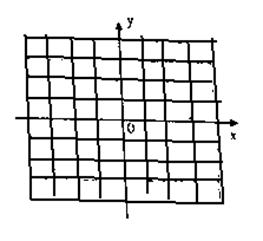
(Ⅰ)作出不等式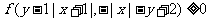 表示的平面区域D,并求其面积.
表示的平面区域D,并求其面积.
(Ⅱ)点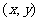 在区域D运动时,求关于x,y的式子
在区域D运动时,求关于x,y的式子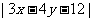 的最大值.
的最大值.
20.已知数列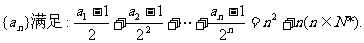
求:
(Ⅰ)数列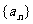 的通项公式;
的通项公式;
(Ⅱ)数列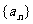 前n项和Sn.
前n项和Sn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com