
5.设等差数列{an}的前n项和是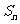 ,且
,且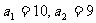 ,那么下列不等式中成立的是
,那么下列不等式中成立的是
( )
A.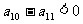 B.
B.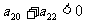 C.
C.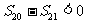 D.
D.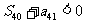
4.在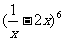 的展开式中
的展开式中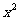 的系数是 ( )
的系数是 ( )
A.240 B.15 C.-15 D.-240
3.将函数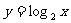 的图象按向量a平移后,得到
的图象按向量a平移后,得到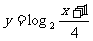 的图象,则 ( )
的图象,则 ( )
A.a=(1,2) B.a=(1,-2) C.a=(-1,2) D.a=(-1,-2)
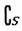 1.已知集合S=R,
1.已知集合S=R,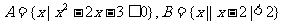 ,那么集合 (A∩B)
,那么集合 (A∩B)
等于 ( )
A.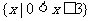 B.
B.
C.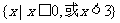 D.
D.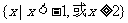
2.在空间中,有如下四个命题:
①平行于同一个平面的两条直线是平行直线;
②垂直于同一条直线的两个平面是平行平面;
③若平面α内有不共线的三个点到平面β距离相等,则α∥β;
④过平面α的一条斜线有且只有一个平面与平面α垂直.
其中正确的两个命题是 ( )
A.①、③ B.②、④
C.①、④ D.②、③
20.(本小题满分14分)
已知:函数f(x)=[x[x]](x∈R),其中[x]表示不超过x的最大整数.
如[-2.1]=-3,[-3]=-3,[2.5]=2.
(1)判断f(x)的奇偶性;
(2)若x∈[-2,3],求f(x)的值域;
(3)若x∈[0,n](n∈N*),f(x)的值域为An,现将An,中的元素的个数记为an.试求an+1与an的关系,并进一步求出an的表达式.
19.(本小题满分14分)
已知:数列{an}的前n项和为Sn,满足Sn=2an-2n(n∈N*)
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=log2(an+2),而Tn为数列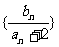 的前n项和,求Tn.
的前n项和,求Tn.
18.(本小题满分13分)
已知:定义域为R的函数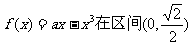 内是增函数.
内是增函数.
(1)求实数a的取值范围;
|
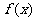 的极小值为-2,求实数a的值.
的极小值为-2,求实数a的值.17.(本小题满分13分)
甲、乙两人各进行3次投篮,甲每次投进的概率为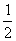 ,乙每次投中的概率为
,乙每次投中的概率为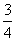 ,求:
,求:
(1)甲恰好投中2次的概率;
(2)乙至少投中2次的概率;
(3)乙恰好比甲多投中2次的概率.
16.(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.过BD作与PA平行的平面BDE,交侧棱PC于点E,又作DF⊥PB,交PB于点F 。
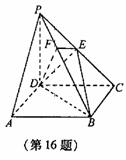 (1)证明:点E是PC的中点;
(1)证明:点E是PC的中点;
(2)证明:PB⊥平面EFD;
(3)求二面有C-PB-D的大小;
15.(本小题满分12分)
在△ABC中,角A、B、C所对的边分别是a、b、c,且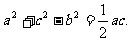
(1)求cosB的值;
(2)求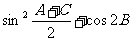 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com