2．双曲线=1的两条准线间的距离等于　　　　　　　　　　　　　　　 (　　 )

　　 A．　　　　　 B．　　　　　 C．　　　　　　 D．

1．化简(2+3i)(3+2i)i(其中i是虚数单位)的结果是　　　　　　　　　　 (　　 )

　　 A．－13i　　　　　 B．13i　　　　　　 C．－13　　　　　 D．13

22．(本题14分)

　 　　　已知等差数列{}中，公差d>0,且前n项和为，又a₂·a₃=45, a₁+a₄=14.

　 　　(1)求{}的通项公式；

　 　　(2)通过构造一个新的数列{}，若{}也是等差数列，求非零常数c．

　　 　(3)求 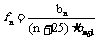(n∈N^*)的最大值。

21．(本题12分)

　　 　已知F₁、F₂是椭圆(a>b>0)的左、右焦点．A是椭圆上位于第一象限内的一点，点B也在椭圆上，且满足OA+OB=0(O是坐标原点)，AF_2·F₁F₂=0。若椭圆的离心率等于。

　　 (1)求直线AB的方程。

　　 (2)若三角形ABF₂的面积等于，求椭圆的方程。

20．(本题12分)

　　 　　　某学校为了解决教师住房问题，计划征用一块土地，盖一幢总建筑面积为am²的宿舍楼．已知土地的征用费为2388元／m²，且每层的建筑面积相同，土地的征用面积为第一层的2．5倍，经工程技术人员核算，第一、二层的建筑费用相同，费用为445元／m²，以后每增高一层，其建筑费用就增加30元／m²．试设计这幢宿舍楼的楼高层数，使总费用最少，并求其最少总费用(总费用为建筑费用和征地费用之和)．

19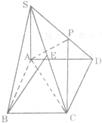．(本题12分)

　　 　　　　如图，在底面是菱形的四棱锥S-ABCD中，∠ABC=60°,SA=AB=a, SB=SD=SA.点P在SD上，且SD=3PD.

　　 　　　　(1)证明SA⊥平面ABCD；

　　 　　　(2)设E是SC的中点，求证BE∥平面APC．

18．(本题12分)

　　 　　　　已知函数f(x)= x²-(ax+b),(a,b∈R)在x=2时有极值，其图像在点(1,f(1))处的切线与直线3x+y=0平行。

　　 　　　　(1)求a,b的值；

　　　　　　 (2)求函数f(x)的单调区间。

17．(本题12分)

　　　　　 　若 a=(), b=(sinx,0),其中〉0，记函数f(x)=(a+b) ·

b +k

　(1)若f(x)图象中相邻两条对称轴间的距离不小于，求的取值范围．

　 　　　　　(2)若f(x)的最小正周期为丌，且当x∈[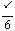，]时，f(x)的最大值是，求f(x)的解析式。

16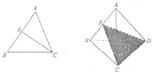．在平面几何中，△ABC的∠C内角平分线CE分AB所成线段的比|AE|:| EB|=| AC|：| CB|．把这个结论类比到空间：在三棱锥A-BCD中(如图)，平面CDE平分二面角A-CD-B且与AB相交于E，可类比得到结论______

15．若函数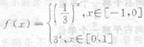则f(log₃)=______________