
19.(本小题满分12分)
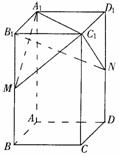 如图,在正四棱柱ABCD-A1B1C1D1中,AB= a,AA1 = 2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB= a,AA1 = 2a,M,N分别是棱BB1,DD1的中点.
(Ⅰ)求异面直线A1M与B1C所成的角的余弦值;
(Ⅱ)求证:平面A1MC1⊥平面B1NC1;
18.(本小题满分12分)
武昌区某中学举行春季运动会,高三某班李萍同学参加女子乒乓球单打比赛.假定从开始的小组淘汰赛到最后决定出冠亚军共经过5轮比赛.若李萍同学在5轮比赛中顺利过关的概率依次为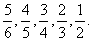 试问:
试问:
(Ⅰ)李萍同学获得该项冠军的可能性有多大?
(Ⅱ)李萍同学在第二轮或第三轮被淘汰的概率是多少?
17.(本小题满分12分)
已知函数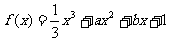 在
在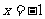 处取得极大值,在x = 3处取极小值.
处取得极大值,在x = 3处取极小值.
(Ⅰ)求f(x)的解析式并指出其单调区间;
(Ⅱ)讨论方程f(x)=k的实根的个数.
16.(本小题满分12分)
已知函数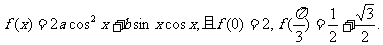
(Ⅰ)求函数f(x)的最大值与最小值;
(Ⅱ)求函数f(x)的单调增区间.
15.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x)的图象恰好通过k个格点,则称函数f (x)为k阶格点函数.下列函数:①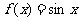 ;②
;②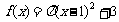 ;③
;③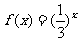 ;④
;④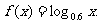 其中是一阶格点函数的有
.(填上所有满足题意的序号)
其中是一阶格点函数的有
.(填上所有满足题意的序号)
14.若函数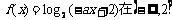 上是减函数,则实数a的取值范围是
.
上是减函数,则实数a的取值范围是
.
13.已知双曲线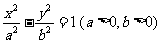 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,
△OAF的面积为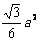 (O为坐标原点),则双曲线的两条渐近线的夹角为
.
(O为坐标原点),则双曲线的两条渐近线的夹角为
.
11.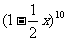 的展开式中x3的系数为
.(用数字作答)
的展开式中x3的系数为
.(用数字作答)
|
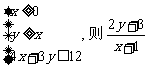 的取值范围是
.
的取值范围是
.10.一次研究性课堂上,老师给出函数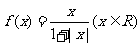 ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1);
乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定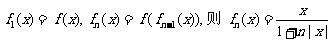 对任意
对任意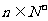 恒成立.
恒成立.
你认为上述三个命题中正确的个数有 ( )
A.0个 B.1个 C.2个 D.3个
第Ⅱ卷(非选择题,共100分)
9.已知函数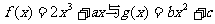 的图象都过点P(2,0),且在点P处有公共切线,则函数g (x)的表达式为 ( )
的图象都过点P(2,0),且在点P处有公共切线,则函数g (x)的表达式为 ( )
A.2x2-4x B.6x2-24 C.-4x2 + 16 D.4x2-16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com