
3.定义域为R的函数 的值域为
的值域为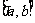 ,则函数
,则函数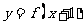 的值域为 ( )
的值域为 ( )
(A)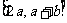 (B)
(B)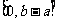 (C)
(C)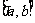 (D)
(D)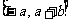
2.若条件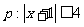 ,条件
,条件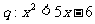 ,则
,则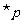 是
是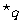 的txjy
的txjy
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分又不必要条件
1.已知集合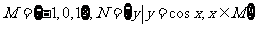 ,则
,则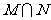 是
(
)
是
(
)
(A)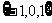 (B)
(B)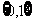 (C)
(C) (D)
(D)
(17)(本小题满分12分)
已知数列{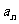 }是首项,
}是首项,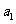 =4、公比
=4、公比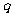 ≠1的等比数列,
≠1的等比数列,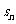 是其前n项和,且4
是其前n项和,且4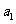 ,
,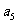 ,-2
,-2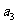 成等差数列.
成等差数列.
(I)求公比q的值;
(Ⅱ)求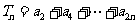 的值.
的值.
(18)(本小题满分12分))
已知函数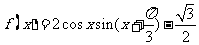
(I)求函数以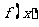 的最小正周期T;
的最小正周期T;
(U)在给定的坐标系中,用“五点法”作出函数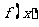 在一个周期上的图象.
在一个周期上的图象.

(19)(本小题满分12分)
甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指头,若和为偶数算甲赢,否则算乙赢.
(I)若以A表示和为6的事件,求P(A);
(Ⅱ)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(Ⅲ)这种游戏规则公平吗?试说明理由.
(20)(本小题满分12分)
一个多面体的直观图及三视图如图所示:(其中M、N别是AF、BC的中点).
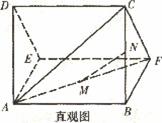 (I)求证:MN//平面CDEF;
(I)求证:MN//平面CDEF;
(Ⅱ)求多面体A-CDEF的体积.
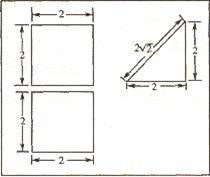
三视图
(21)(本小题满分12分)
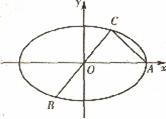
如图,已知A、B、C是椭圆E: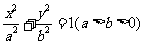 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为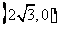 ,BC过椭圆的中心0,且AC⊥BC,
,BC过椭圆的中心0,且AC⊥BC,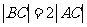 .
.
(I)求点C的坐标及椭圆E的方程;
 (Ⅱ)若椭圆E上存在两点P、Q,使得直线PC与直线QC关于直线
(Ⅱ)若椭圆E上存在两点P、Q,使得直线PC与直线QC关于直线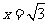 对称,求直线PQ的斜率.
对称,求直线PQ的斜率.
(22)(本小题满分14分)
已知函数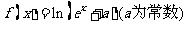 是实数集R上的奇函数,函数
是实数集R上的奇函数,函数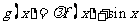 是区间[一1,1]上的减函数.
是区间[一1,1]上的减函数.
(I)求a的值;
(II)求A的取值范围;
(Ⅲ)若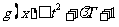 在x∈[一1,1]上恒成立,求t的取值范围.
在x∈[一1,1]上恒成立,求t的取值范围.
 (13)某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是
(13)某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是
(14)在Rt△ABC中,∠C=90°,∠A=30°,则以A、B为焦点,过点C的椭圆的离心率是
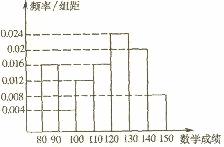
(15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图).则这10000人中数学成绩在[140,150]段的约是 。
 (16)一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于 cm3.
(16)一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于 cm3.
(1)复数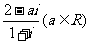 是纯虚数,则
是纯虚数,则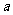 =
=
(A)0 (B)1 (C)2 (D)3
(2)抛物线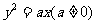 的焦点到其准线的距离是
的焦点到其准线的距离是
(A)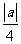 (B)
(B)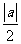 (c)
(c)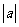 (D)
(D)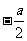
(3)用二分法研究函数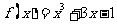 的零点时,第一次经计算
的零点时,第一次经计算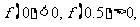 可得其中一个零点
可得其中一个零点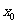 ∈ ,第二次应计算
.以上横线上应填的内容为
∈ ,第二次应计算
.以上横线上应填的内容为
(A)(0,0.5),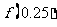 (B)(0,1),
(B)(0,1),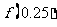
(C)(0.5,1),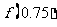 D)(0,0.5),
D)(0,0.5),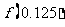
(4)若函数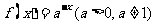 是定义域为R的增函数,则函数
是定义域为R的增函数,则函数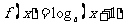 的图象大致是
的图象大致是
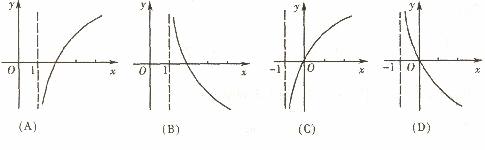
(5)已知a,b表示直线,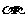 表示平面,则a∥
表示平面,则a∥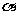 的一个充分条件是
的一个充分条件是
(A)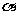 //
//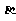 ,
,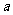 //
//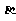 (B)
(B)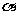 ⊥
⊥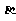 ,
,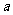 ⊥
⊥
(C)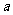 //
//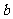 ,
,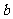 //
//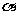 (D)
(D)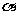
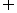
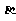 =
=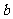 ,
,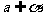 ,
,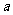 //
//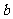
(6)过抛物线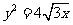 的焦点,且与圆
的焦点,且与圆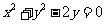 相切的直线方程是
相切的直线方程是
(A)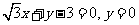
(B)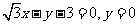
(C)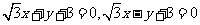
(D)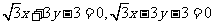
(7)已知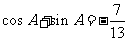 ,A为第四象限角,则ta
nA等于
,A为第四象限角,则ta
nA等于
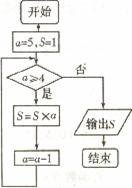 (A)
(A)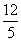 (B)
(B)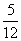 (C)
(C)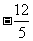 (D)
(D)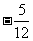
(8)右面的程序框图输出的结果是
(A)5
(B)10
(C)15
(D)20
(9)已知函数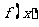 是以2为周期的偶函数,且当石
是以2为周期的偶函数,且当石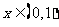 时,
时,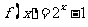 ,则
,则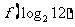 的值为
的值为
(A)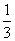 (B)
(B) 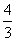 (C)2 (D)11
(C)2 (D)11
(10)设0<a<b<1,且a+b=1,给出下列结论:
①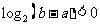 ②
②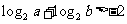
③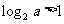 ④
④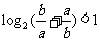
其中正确结论的个数是
(A)1个 (B)2个 (C)3个 (D)4个
(11)已知等差数列{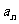 }的前n项和为
}的前n项和为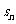 ,若
,若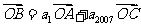 ,且A、B、C三点共线(0为该直线外一点),则
,且A、B、C三点共线(0为该直线外一点),则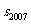 =
=
(A)2007 (B)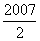 (C)
(C)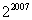 (D)
(D) 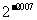
(12)点P是双曲线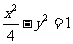 的右支上一点,M、N分别是圆
的右支上一点,M、N分别是圆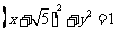 和圆
和圆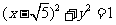 上的点,则
上的点,则 的最大值是
的最大值是
(A)2 (B)4 (C)6 (D)8
第Ⅱ卷 (非选择题共90分)
22.(18分)对于区间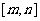 上有意义的两个函数
上有意义的两个函数 均有
均有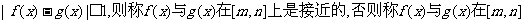 上是非接近的。
上是非接近的。
现有两个函数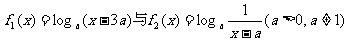
(1)求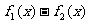 的定义域;
的定义域;
(2)若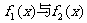 在整个给定区间
在整个给定区间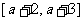 上都有意义,
上都有意义,
①求a的取值范围;
②讨论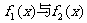 在整个给定区间
在整个给定区间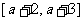 上是不时是接近的。
上是不时是接近的。
21.(16分)现有一批货物从上海洋山深港运往青岛,已知该船的最大航行速度为35海里/小时,上海至青岛的航行距离约为500海里,每小时的运输成本由燃料费用和其余费用组成。轮船每小时使用的燃料费用与轮船速度的平方成正比(比例系数为0.6),其余费用为每小时960元。
(1)把全程运输成本y(元)表示为速度x(海里/小时)的函数;
(2)为了使全程运输成本最小,轮船应以多大速度行驶?
20.(14分)设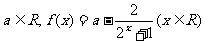
(1)确定a的值,使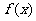 为奇函数;
为奇函数;
(2)当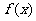 是奇函数时,设
是奇函数时,设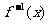 为函数
为函数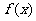 的反函数,则对给定的正实数k,求使
的反函数,则对给定的正实数k,求使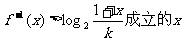 的取值范围。
的取值范围。
19.(14分)已知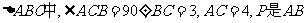 的动点,求点P到AC,BC距离乘积的最大值。
的动点,求点P到AC,BC距离乘积的最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com