
7.有5个不同的红球和2个不同的黑球排成一列,在两端都有红球的排列中,其中红球甲和黑球乙相邻的排法有 ( )
A.720 B.768 C.960 D.1440
6.命题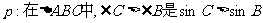 的充分必要条件;
的充分必要条件;
|
 的充分不必要条件 ( )
的充分不必要条件 ( )
A.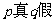 B.
B.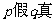
C.“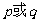 ”为假 D.“
”为假 D.“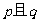 ”为真
”为真
5.函数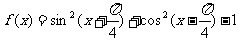 是 ( )
是 ( )
A.周期为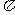 的奇函数 B.周期为
的奇函数 B.周期为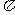 的偶函数
的偶函数
C.周期为2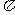 的奇函数 D.周期为2
的奇函数 D.周期为2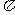 的偶函数
的偶函数
4.将函数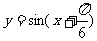 的图象按向量
的图象按向量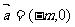 平移所得的图象关于
平移所得的图象关于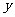 轴对称,则
轴对称,则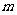 最小正值是 ( )
最小正值是 ( )
A.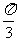 B.
B.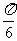 C.
C.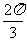 D.
D.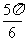
3.已知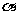 、
、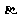 是两个不同平面,
是两个不同平面,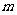 、
、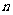 是两不同直线,下列命题中的假命题是 ( )
是两不同直线,下列命题中的假命题是 ( )
A.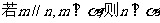 B.
B.
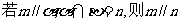
C.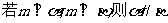 D.
D. 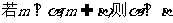
2.函数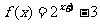 的反函数图象经过Q点,则Q点的一个坐标是 ( )
的反函数图象经过Q点,则Q点的一个坐标是 ( )
A.(1,2) B.(3,1) C.(4,2) D.(5,2)
1.设全集U=R,集合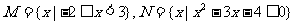 ,则
,则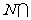
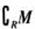 等于( )
等于( )
A.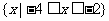 B.
B.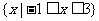
C.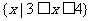 D.
D.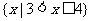
20.(本小满分14分)
已知函数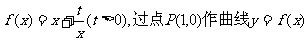 的两条切线PM、PN,切点
的两条切线PM、PN,切点
分别为M、N.
(I)当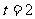 时,求函数
时,求函数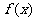 的单调递均区间;
的单调递均区间;
(II)设|MN|=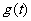 ,试求函数
,试求函数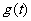 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数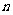 ,在区间
,在区间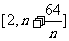 内总存在
内总存在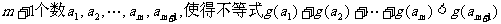 成立,求m的最大值.
成立,求m的最大值.
19.(本小题满分13分)
已知平面上两定点M(0,-2)、N(0,2),P为一动点,满足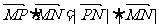 .
.
(I)求动点P的轨迹C的方程;
(II)若A、B是轨迹C上的两不同动点,且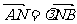 . 分别以A、B为切点作轨迹C的切线,设其交点Q,证明
. 分别以A、B为切点作轨迹C的切线,设其交点Q,证明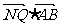 为定值.
为定值.
18. (本小题满分14分)
(本小题满分14分)
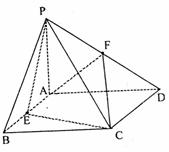
如图,四棱锥P-ABCD中,PA⊥ABCD,
四边形ABCD是矩形. E、F分别是AB、PD的
中点.若PA=AD=3,CD=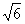 .
.
(I)求证:AF//平面PCE;
(II)求点F到平面PCE的距离;
(III)求直线FC与平面PCE所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com